题目描述

Hobson 先生从管理马厩的工作中退休后，投资于一种更加现代的交通方式：火车。

他已经修建了一个包含 $n$ 个火车站的铁路网。然而，他兑现了让乘客摆脱选择困难症的承诺：对于每个站点，乘客只能乘坐火车前往一个站点，别无其它选择。

这样的一段旅程被称作一趟。要注意这是单向的旅程，可能无法再回到出发点。

Hobson 同样也只提供一种车票，允许乘客一次旅行的距离不超过 $k$ 趟。在每个站点的出口会有一个自动读票机（只有一个，所以乘客就不用纠结于要用哪个）。机器会检查从始发站到到达站的距离是否不超过 $k$ 趟。

每个读票机必须编入一个合法始发站列表，但是列表消耗的存储空间越多，机器就越贵。

请帮助 Hobson 先生确定：对于每个站点 $A$，能够在最多 $k$ 趟的旅程中到达 $A$ 的站点个数（包含 $A$ 本身）。

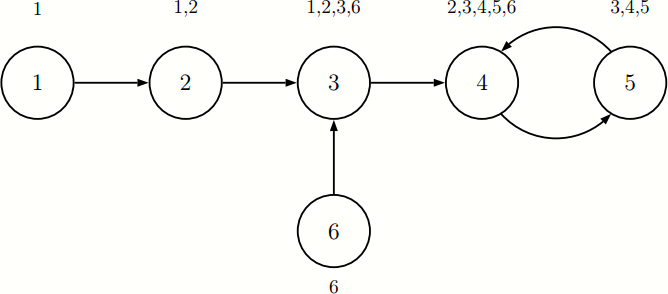
上图为样例输入 1 对应的示意图。每个圆圈代表了一个站点，圆圈旁边的数字为当 $k=2$ 时需要编入读票机的站点编号。

输入格式

第一行包含两个整数 $n, k$，$n$ 为站点个数，$k$ 为一张票允许旅行的最多趟数。
接下来 $n$ 行，第 $i$ 行包含一个整数 $d_i$，表示第 $i$ 个站点经过一趟到达的站点。

输出格式

输出 $n$ 行，第 $i$ 行输出能在 $k$ 趟内到达站点 $i$ 的站点数目。

样例 1

input

6 2
2
3
4
5
4
3

output

1
2
4
5
3
1

样例 2

input

5 3
2
3
1
5
4

output

3
3
3
2
2

数据范围与提示

$2\le n\le 5\cdot 10^5$

$1\le k\le n-1$

$1\le d_i\le n$，$d_i\neq i$

在不侵犯原题版权的情况下，本题面中文翻译基于知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议发布，注明出处时需指向本题链接。