题目描述

你家乡的议会决定对一些道路标志的安置进行改进，特别是一些断头路。他们给了你一个地图，你必须确定在哪里贴上「此路不通」标志，他们希望你使用的标志尽可能少。

地图是由双向街道连接一些地点而形成的集合。以下规则描述了在一个街道 $ S $ 的入口 $ x $ 安放一个「此路不通」标志的条件：如果在从 $ x $ 点进入街道 $ S $ 后，只能通过掉头的方式回到 $ x $，就应该安装一个「此路不通」标志。定义一个「掉头」操作为做一个 $180$ 度的转弯，即立刻反转行车的方向。

为了节省成本，你决定不安装任何多余的标志。如果一个街道 $ S $ 的入口 $ x $ 有一个「此路不通」标志，另一条街道 $ T $ 的入口 $ y $ 有一个「此路不通」标志，如果从 $ x $ 点进入街道 $ S $ ，并能在不掉头的情况下经过 $ y $ 点进入街道 $ T $ ，那么 $ T $ 的入口 $ y $ 处的标志就是多余的。

输入格式

输入的第一行包含两个整数 $ n,m $，分别代表图中地点的数目和街道的数目。

接下来 $ m $ 行，每行包含两个整数 $ v,w $，表示这条街道连接了 $ u,v $ 两个地点。

输入保证不会给出重复的街道。

输出格式

第一行输出一个数字 $ k $ ，代表安装的「此路不通」标志的数量。

接下来 $ k $ 行，每行输出两个整数 $ v,w $，代表在连接 $ v,w $ 的街道的 $ v $ 入口处安装一个「此路不通」标志。

输出的街道应该先按 $ v $ 的升序进行排列，当 $ v $ 相同的时候，按照 $ w $ 的升序排列。

样例 1

input

6 5
1 2
1 3
2 3
4 5
5 6

output

2
4 5
6 5

本样例对应下图：

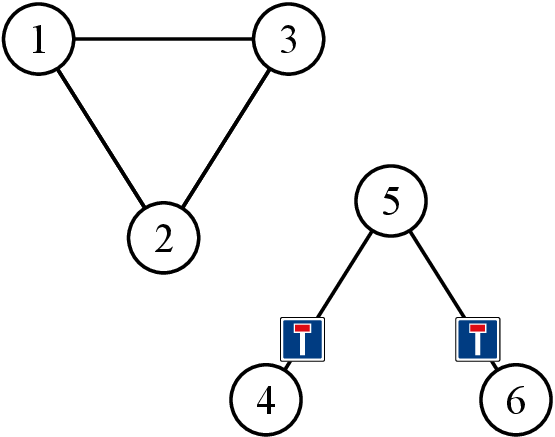
样例 2

input

8 8
1 2
1 3
2 3
3 4
1 5
1 6
6 7
6 8

output

3
1 5
1 6
3 4

本样例对应下图：

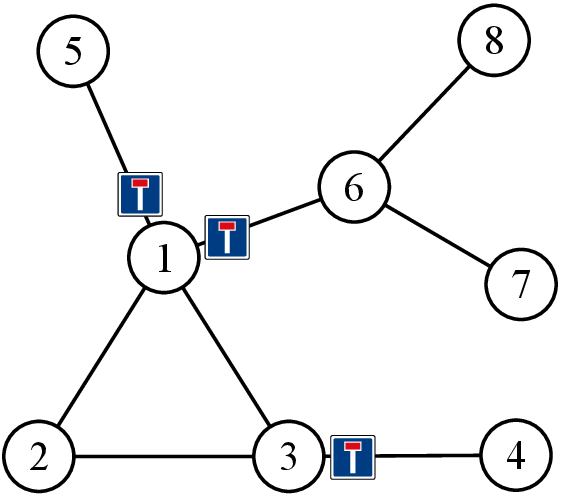
数据范围与提示

$ 1 \leq n \leq 5 \times 10^5, 0 \leq m \leq 5 \times 10^5 , 1 \leq v < w \leq n $