题目描述

这道题目非常简单，它甚至没有题目背景、没有任何故事。

但为了能让你顺利理解题目，善良的 Yazid 将为你介绍一些概念。

• 简单图：不存在重边、自环的图。（重边即为两条完全相同的边，自环即为两端点为同一节点的边）

• 补图：一个图 $G$ 的补图有与 $G$ 完全相同的节点，且任意两点之间有边当且仅当他们在 $G$ 中不相邻。

我们归纳定义一个无向简单图是好的：

1. 一个单点是好的。

2. 若干个好的图分别作为联通块所形成的图是好的。

3. 一个好的图的补图是好的。

给定一个正整数 $n$。

求 $n$ 个点的本质不同的好的图的数量对质数 $P$ 取模的结果。（这里的 $P$ 是一个常数，具体见【输入格式】）

两个好的图的被认为是本质不同的，当且仅当无论如何将一个图重标号，它都不能与另一个图完全相同。

输入格式

输入包含多组数据，第一行 $2$ 个用空格隔开的整数 $T,P$ 分别表示数据组数、以及模数。接下来依次描述每组数据，对于每组数据：

• 一行一个整数 $n$，表示希望统计数目的好的图的节点数。

输出格式

对于每组数据，输出 $1$ 行：

• 一个整数，表示 $n$ 个节点的好的图的数目对 $P$ 取模的结果。

样例

input

2 233
3
4

output

4
10

下面是 $3$ 个点的所有好的图：

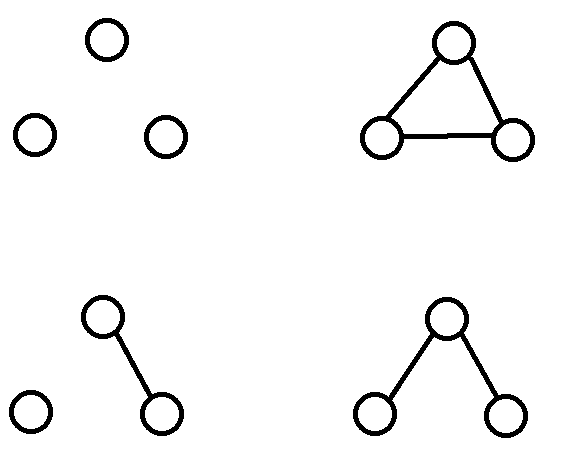
数据范围与提示

保证 $T\leq 233$，$n\leq 23333$，$2^{29} < P < 2^{30}$ 且保证 $P$ 为质数。

能够通过本题的算法的时间复杂度可能比你想象的要糟糕一些、也可能比你想象的要优秀一些。

来自 2018 清华大学学生程序设计竞赛暨高校邀请赛（THUPC2018），感谢 Pony.ai 对此次比赛的支持。

题解等资源可在 https://github.com/wangyurzee7/THUPC2018 查看。