题目描述

阿尔卡狄决定连续 $n$ 天观察一条河流。这条河流每天的水位都是一个实数。

每天早上，阿尔卡狄来到河岸边，并在河道边上的水位处作一个标记，但是在水位恰好和已有标记重合的情况下不作重复记录。第一天之前河道上没有标记，并且水流不会冲刷掉标记。

每天阿尔卡狄都会记录下严格在水面以上的标记数量，第 $i$ 天的这个数目是 $m_i$。

用 $d_i$ 表示第 $i$ 天严格在水面以下的标记数量。请计算所有 $d_i$ 之和的最小值。

输入格式

输入的第一行包含一个正整数 $n$ —— 记录的天数。

第二行包含 $n$ 个空格分隔的整数 $m_1, m_2, \ldots, m_n$ —— 第 $i$ 天严格在水面以上的标记数量。

输出格式

输出一行，包含一个整数，表示所有水面以下标记数目之和的最小值。

样例 1

input

6
0 1 0 3 0 2

output

6

样例 1 的一个最优情况如下所示。

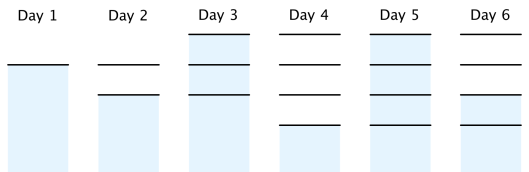
在第 $3$ 天必须有一个新的标记是因为若不然，第 $4$ 天不能有 $3$ 个水面上的标记。水面以下的标记数目之和为 $0 + 0 + 2 + 0 + 3 + 1 = 6$。

样例 2

input

5
0 1 2 1 2

output

1

样例 2 的一个最优情况如下所示。

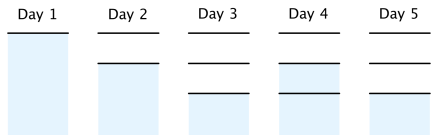
样例 3

input

5
0 1 1 2 2

output

0

数据范围与提示

$1 \leq n \leq 10^5$
$0 \leq m_i \lt i$