题目描述
いつまでも止まらない この胸のときめきで 一緒に踊ろう
随着永不停息的这心中的悸动,一起来跳舞吧!
给定坐标平面上 $n$ 个圆。任意两个圆的边界至多只有一个公共点 —— 即它们必定相离或相切。
对于一个圆的集合,定义其异或面积为平面上被该集合中奇数个圆覆盖的图形面积。
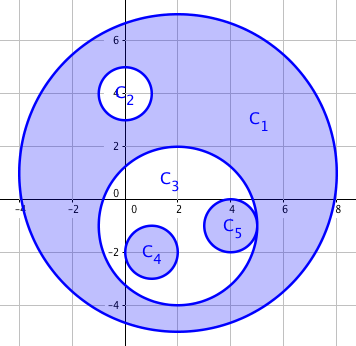
对于这个集合,浅蓝色部分图形的面积被计入异或面积内。
现在需要将这 $n$ 个圆划分为两个集合,每个圆恰好在两个集合中的一个内。
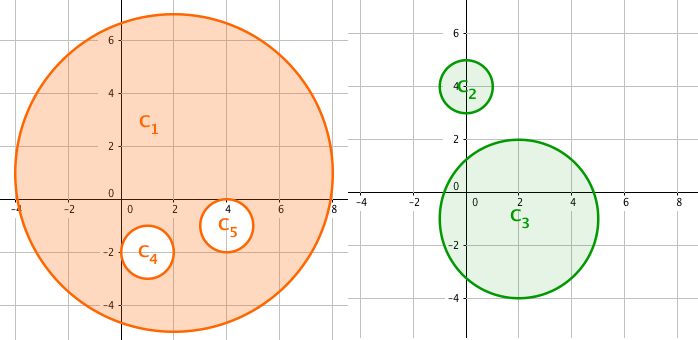
一种划分的方案,两个集合的异或面积如图所示。
请求出合法的划分方案中,两个集合分别计算的异或面积之和的最大值。
输入格式
输入的第一行包含一个正整数 $n$ —— 圆的数目。
接下来 $n$ 行,每行包含三个整数 $x_i, y_i, r_i$ —— 描述一个圆心位于 $(x_i, y_i)$、半径为 $r_i$ 的圆。
输出格式
输出一个十进制实数 —— 合法的划分方案中,两个集合异或面积之和的最大值。
当选手答案与参考答案的相对误差或绝对误差不超过 $10^{-9}$ 时被视为正确。形式化地,若选手输出为 $a$,参考答案为 $b$,答案被视为正确当且仅当 $\frac{|a-b|}{\max{(1, |b|)}} \le 10^{-9}$。
样例 1
input
5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1output
138.23007676
样例 1 的最优方案与「题目描述」一节中的图形对应。
样例 2
input
8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8output
289.02652413
数据范围与提示
$1 \leq n \leq 1\,000$
$-10^6 \leq x_i, y_i \leq 10^6$,$1 \leq r_i \leq 10^6$
ささやかだけど かけがえのない 歴史を重ねて
渺小平凡却无可替代的事物一点点重现着历史
偽りさえも 本当になる 君の隣りで
即使谎言在你身旁也会变得如此真实
——「白金ディスコ」
* 熬夜有害身体健康
