题目描述
译自 CCO 2020 Day1 T3「Mountains and Valleys」,翻译者:PinkRabbit。
给定一张 $N$ 个点 $M$ 条边的无向图,节点的标号为 $0 \sim (N - 1)$,其中边有正整数边权。
特别地,有恰好 $N - 1$ 条边的边权为 $1$,且仅考虑这些边时,图形成了一棵树。而对于其它边,它们的边权至少为 $\displaystyle \left\lceil \frac{N}{3} \right\rceil$。
请你找出一条路径,可以从任意节点出发,并最终在任意节点停下,但需要经过每一个节点至少一次,且最小化总边权。注意,如果你经过一条边权为 $d$ 的边 $k$ 次,那么这条边会为总边权贡献 $k \cdot d$。
输入格式
第一行两个正整数 $N, M$。
接下来 $M$ 行,每行三个正整数 $x_i, y_i, w_i$,表示一条连接着节点 $x_i$ 和 $y_i$ 的边权为 $w_i$ 的边。
输出格式
输出一行一个数表示最小的总边权。
样例
input
9 10
0 1 1
0 2 1
0 3 1
1 4 1
2 5 1
2 6 1
3 7 1
3 8 1
2 4 5
6 7 3output
11
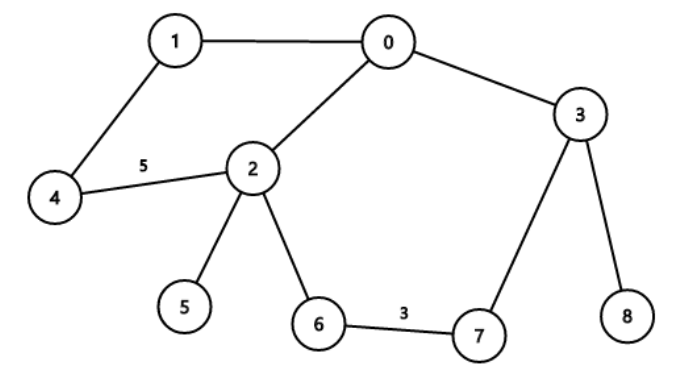
最优方案之一为路径 $4 \to 1 \to 0 \to 2 \to 5 \to 2 \to 6 \to 7 \to 3 \to 8$,总边权为 $1 + 1 + 1 + 1 + 1 + 1 + 3 + 1 + 1 = 11$。不存在总边权更小的能够经过每个点至少一次的路径。
数据范围与提示
对于所有数据,保证 $4 \le N \le 5 \times {10}^5$,$N - 1 \le M \le 2 \times {10}^6$,$0 \le x_i, y_i < N$,$w_i = 1$ 或 $\displaystyle \left\lceil \frac{N}{3} \right\rceil \le w_i \le N$,无重边或自环。
| 子任务编号 | 分值 | $N \le$ | $M \le$ | 特殊限制 |
|---|---|---|---|---|
| $1$ | $4$ | $6$ | $10$ | 无特殊限制 |
| $2$ | $8$ | $20$ | $40$ | 无特殊限制 |
| $3$ | $8$ | $5000$ | $10000$ | $w_i = 1$ 或 $\displaystyle \left\lceil \frac{N}{2} \right\rceil \le w_i \le N$ |
| $4$ | $24$ | $100$ | $200$ | 无特殊限制 |
| $5$ | $8$ | $500$ | $1000$ | 无特殊限制 |
| $6$ | $12$ | $5000$ | $10000$ | 无特殊限制 |
| $7$ | $20$ | $80000$ | $160000$ | 无特殊限制 |
| $8$ | $16$ | 无特殊限制 | 无特殊限制 | 无特殊限制 |
