题目描述
题目译自 POI XXVII - I etap 「Układ scalony」
有一个 $n \cdot m$ 个点排成 $n$ 行 $m$ 列,其中第 $i$ 行第 $j$ 列的坐标为 $(i, j)$。对于两个点 $(x_1,y_1)$ 和 $(x_2,y_2)$,如果 $|x_1-x_2| + |y_1-y_2|=1$,那么它们之间有一条边相连。
给定一个整数 $k$,你需要找到这个图的一个生成树,使得它的直径上恰好有 $k$ 条边。
输入格式
输入仅一行包含三个整数 $n$,$m$ 和 $k$。
输出格式
如果不存在这样的生成树,输出 NIE。否则,在第一行输出 TAK。接下来 $nm-1$ 行,每行包含 $4$ 个整数 $i_1,j_1,i_2,j_2$ ($1 \le i_1, i_2 \le n, 1 \le j_1, j_2 \le m$),表示点 $(i_1,j_1)$ 和点 $(i_2,j_2)$ 之间有边相连。如果有多组解,输出任意一组即可。
样例 1
input
2 3 4output
TAK
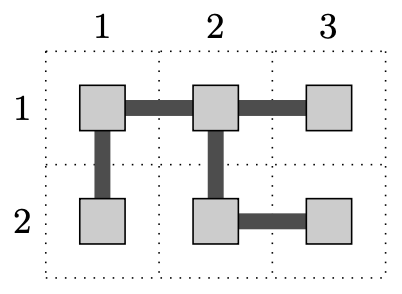
1 1 1 2
1 1 2 1
1 2 2 2
2 3 2 2
1 2 1 3
样例 2
input
2 3 1output
NIE
附加样例参见 ukl/ukl*.in 和 ukl/ukl*.out:
-
附加样例 $1$:$n=2,m=3,k=3$;
-
附加样例 $2$:$n=1,m=10,k=10$;
- 附加样例 $3$:$n=1000,m=1000,k=999\ 999$。
数据范围与提示
对于 $100\%$ 的数据,$1 \le n, m \le 1000, 0 \le k \le 10^6$。
| Subtask # | 限制 | 分值 |
|---|---|---|
| 1 | $n,m\le 6$ | 20 |
| 2 | $n \le 3, m \le 1000$ | 20 |
| 3 | $n,m \le 1000$,$n \cdot m$ 是奇数 | 30 |
| 4 | $n,m \le 1000$,$n \cdot m$ 是偶数 | 30 |
