题目描述

题目译自 USACO 2019 December Contest, Platinum Problem 3. Tree Depth

为了迎接新年，Farmer John 决定给他的奶牛们一个节日二叉搜索树！

为了生成这个二叉搜索树，Farmer John 从一个 $1\ldots N$ 的排列 $a={1,2,\ldots ,N}$ 开始，然后以参数 $1$ 和 $N$ 开始运行如下的伪代码：

generate(l,r):
  if l > r, return empty subtree;
  x = argmin_{l <= i <= r} a_i; // index of min a_i in {a_l,...,a_r}
  return a BST with x as the root, 
    generate(l,x-1) as the left subtree,
    generate(x+1,r) as the right subtree;

例如，排列 ${3,2,5,1,4}$ 将产生如下的二叉搜索树：

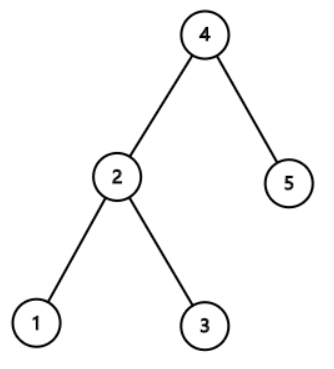
令 $d_i(a)$ 表示节点 $i$ 在用排列 $a$ 生成的二叉搜索树中的深度。深度定义为这个节点到根节点的路径上的点数。在上述例子中，$d_4(a)=1,d_2(a)=d_5(a)=2,d_1(a)=d_3(a)=3$。

$a$ 中的逆序对数等于满足 $1\le i<j\le N$ 且 $a_i>a_j$ 的数对 $(i,j)$ 的个数。奶牛们知道 Farmer John 用来生成二叉搜索树的排列 $a$ 中恰好有 $K$ 个逆序对。对于所有满足条件的 $a$，请计算对于每个 $1\le i\le N$，$\sum_a d_i(a)$ 对 $M$ 取模后的结果。

输入格式

输入只有一行，包含三个整数 $N,K,M$。

输出格式

输出一行 $N$ 个整数，第 $i$ 个整数表示 $\sum_a d_i(a)\pmod M$。两个整数之间用一个空格隔开。

样例 1

input

3 0 192603497

output

1 2 3

对于这个样例，唯一满足条件的排列为 $a={1,2,3}$。

样例 2

input

3 1 144408983

output

3 4 4

对于这个样例，满足条件的两个排列分别为 $a={1,3,2}$ 和 $a={2,1,3}$。

数据范围与提示

对于全部数据，$1\le N\le 300,0\le K\le \frac{N(N-1)}{2}$，保证 $M$ 是一个 $[10^8,10^9+9]$ 范围中的质数。

对于测试点 $3,4$，满足 $N\le 8$；

对于测试点 $5\sim 7$，满足 $N\le 20$；

对于测试点 $8\sim 10$，满足 $N\le 50$。