题目描述
本题译自 eJOI2019 Problem C. T - Covering
如果你玩过俄罗斯方块,应该见过如下图形:
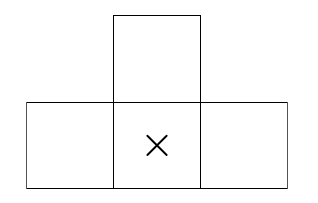
我们称它为一个 T 形四格拼板。其中心被标记为 $\times$。
Manca 画了一个 $m$ 行 $n$ 列的长方形网格,行从 $0$ 至 $m-1$ 编号,列从 $0$ 至 $n-1$ 编号。其中每个格子上填有一个数。她将其中一些格子标记为特殊格子,接下来她向你询问一种在格子中放入 T 形四格拼板的方案,需满足:
- 每个标记的格子恰是一个 T 形四格拼板的中心,其他位置不许放置拼板。
- T 形四格拼板之间不能有重叠部分。
- 所有拼板的部分均在网格内。
注意,T 形四格拼板有四种摆放方式:$\top, \bot, \vdash, \dashv$。
如果方案不存在,输出 No,否则请找出一种方案使得被拼板覆盖的数总和最大。
输入格式
第一行输入两个正整数 $m, n$,表示行数和列数。
接下来 $m$ 行,每行输入 $n$ 个整数,第 $i$ 行第 $j$ 个数(从 $0$ 开始编号)表示对应 $i$ 行 $j$ 列上的数 $a_{ij}$。
接下来一行输入一个正整数 $k$,表示被标记的格子数量。
接下来 $k$ 行,每行两个整数 $r_i, c_i$ 表示第 $i$ 个被标记的格子,保证坐标互不相同。
输出格式
如果有方案,输出可能的被覆盖的格子内数总和的最大值,否则输出 No。
样例 1
input
5 6
7 3 8 1 0 9
4 6 2 5 8 3
1 9 7 3 9 5
2 6 8 4 5 7
3 8 2 7 3 6
3
1 1
2 2
3 4output
67
为了使总和最大,一种方案是这样的:
- $(1, 1)$ 位置放置方向为 $\dashv$。
- $(2, 2)$ 位置放置方向为 $\vdash$。
- $(3, 4)$ 位置放置方向为 $\bot$。
样例 2
input
5 6
7 3 8 1 0 9
4 6 2 5 8 3
1 9 7 3 9 5
2 6 8 4 5 7
3 8 2 7 3 6
3
1 1
2 2
3 3output
No
数据范围与提示
对于 $100\%$ 的数据,保证 $1\le k\le nm \le 10^6, 0\le a_{ij}\le 10^3$。
| 子任务编号 | $k$ | 特殊限制 | 分值 |
|---|---|---|---|
| $1$ | $\le 10^3$ | 保证对于 $i\neq j$,$\max(\vert r_i - r_j\vert, \vert c_i - c_j\vert) > 2$ | $5$ |
| $2$ | $\le 10^3$ | 保证对于 $i\neq j$,若 $\max(\vert r_i - r_j\vert, \vert c_i - c_j\vert)\le 2$,则 $(r_i, c_i)$ 与 $(r_j, c_j)$ 有相邻边 | $10$ |
| $3$ | $\le 10^3$ | 保证对于 $i\neq j$,$\max(\vert r_i - r_j\vert, \vert c_i - c_j\vert) \neq 2$ | $10 $ |
| $4$ | $\le 10^3$ | 所有特殊格子在同一行 | $10$ |
| $5$ | $\le 10$ | $15$ | |
| $6$ | $\le 10^3$ | $20$ | |
| $7$ | $30$ |
