题目描述
译自 ROI 2019 Day2 T3. Робогольф
高尔夫球赛的场地是一个长方形,长方形被划分为 $n$ 行,每行 $m$ 个单元格,行依次编为 $1\ldots n$ 号,列依次编为 $1\ldots m$ 号。可以用数对 $(r,c)$ 来指明场上的任意一个单元格,$r,c$ 分别表示该单元格所在的行、列的编号。有 $k$ 个单元格有球洞。
两人(机器人)交替挥杆。如果球在 $(r,c)$,人可以把球打到 $(r,c+1)$ 或 $(r+1,c)$。如果球到了第 $n$ 行或第 $m$ 列,人可以将其打到场外。只要球被打到了有球洞的单元格,就视为进洞。如果球离开了场地或进洞了,比赛结束。
每个洞会有一个分值 $v_i$,可能是负数。比赛得分为球进的洞的分值,如果被打出场外则分值为 0。先手希望得分越小越好,后手希望得分越大越好。
用 $g(r,c)$ 表示一场在 $(r,c)$ 发球的比赛。$g(r,c)$ 的期望结果等于这场比赛的最小可能得分。特别的,如果 $(r,c)$ 有球洞,则 $g(r,c)$ 的期望结果等于该场比赛期望结果取决于先手,与后手无关(?)。
试求所有 $g(r,c)$ 的期望结果之和。答案对 $998\ 244\ 353$ 取模。
输入格式
$n,m,k$
接下来 $k$ 行,每行三个整数 $r_i,c_i,v_i$,表示 $(r_i,c_i)$ 上有一个球洞,其分值为 $v_i$。
样例 1
input
3 3 3
2 3 -2
3 1 3
1 2 1output
998244352
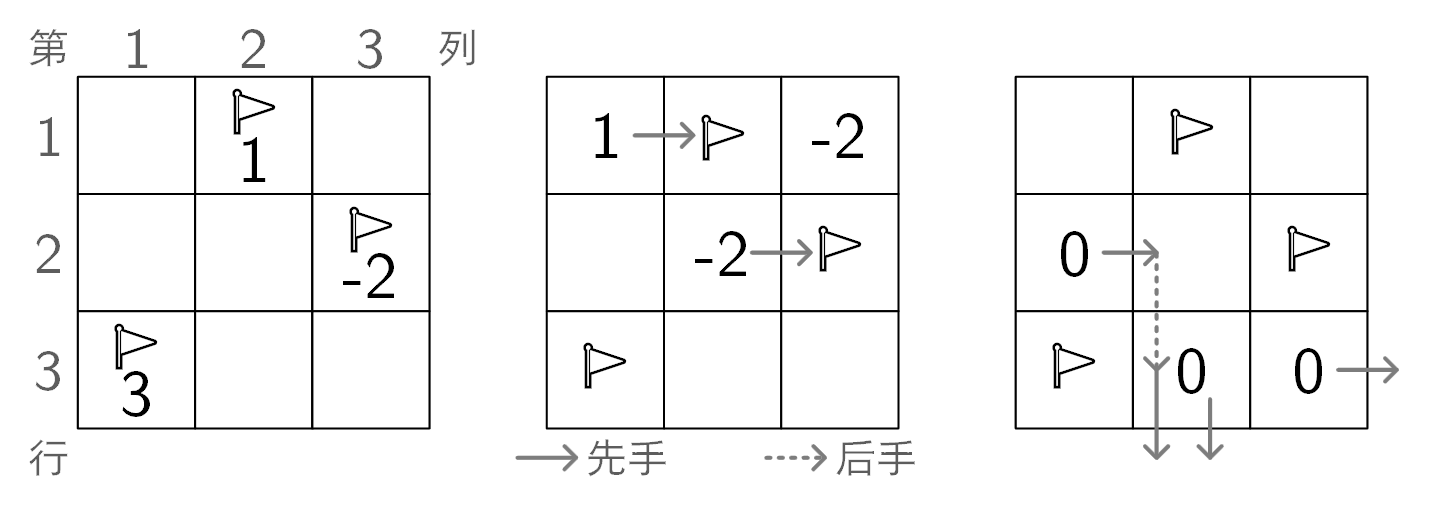
总和为 $1 + 1 − 2 + 0 − 2 − 2 + 3 + 0 + 0 = −1$。
样例 2
input
2 4 3
1 2 2
2 4 -3
2 1 1output
998244348

$1 + 2 + 0 − 3 + 1 + 0 − 3 − 3 = −5$
数据范围与提示
$1 ⩽ n, m ⩽ 10^9$; $1 ⩽ k ⩽ \min(n · m, 10^5)$; $−10^9 ⩽ v_i ⩽ 10^9$。
| 子任务 # | 分值 | $n,m$ | $k$ | 附加条件 |
|---|---|---|---|---|
| 1 | 20 | $n,m⩽1000$ | $$ | |
| 2 | 14 | $n ⩽ 5, m ⩽ 10^9$ | $$ | |
| 3 | 14$$ | $n,m⩽10^5$ | $k = n + m − 1$ | $\forall i,$ $r_i=n$ 或 $c_i=m$ |
| 4 | 10 | $\forall i,$ $r_i⩾ n − 1 000$ 或 $c_i⩾ n − 1 000$ | ||
| 5 | 6 | $n,m⩽10^5$ | $\forall i,$ $v_i=1$ | |
| 6 | 6$$ | $\forall i,$ $v_i=1$ | ||
| 7 | 10 | $n,m⩽10^5$ | ||
| 8 | 10$$ | $k ⩽ 1 000$ | ||
| 9 | 10 |
