题目描述
很抱歉,由于技术局限,本题仅支持各版本 C++。
提示:请参考选手目录下的示例代码,int[] 的实际实现方式为 std::vector<int>,int64 的实际实现方式为 long long。
德黑兰市是伊朗国家图书馆的所在地。这个图书馆的镇馆之宝位于一个长长的大厅内,大厅里有排成一行的 $n$ 张桌子,从左到右依次编号为从 $0$ 到 $n-1$。每张桌子上都陈列着一本手写的古书。这些古书是根据其历史年份进行排序的,这使得访客们难以根据书名来查找它们。所以,图书馆主管决定按照书名的字母序来重新排列它们。
图书管理员 Aryan 要完成这项工作。他创建了一个长度为 $n$ 的列表 $p$,其中包括由 $0$ 到 $n-1$ 的不同整数。这个列表描述了按字母序来重排古书所要做的改变:对于 $0\le i<n$,目前在桌子 $i$ 上的古书应该被移到桌子 $p[i]$ 上。
Aryan 从桌子 $s$ 开始重排这些古书。他希望在做完重排工作之后再回到同一张桌子上。由于这些古书非常珍贵,在任何时间,他手持的古书都不能超过一本。在重排古书的过程中,Aryan 将会做一系列的操作。每个操作只能是以下其中之一:
- 如果他手上没有书,而他所在的桌子上恰好有一本书时,他可以拿起这本书。
- 如果他手上有一本书,而他所在的桌子上恰好有另一本书时,他可以把手上的书和桌子上的书进行交换。
- 如果他手上有一本书,而他所在的桌子上没有书时,他可以把手上的书放到这个桌子上。
- 他可以走到任何一张桌子前。当他进行这个操作时,他手上可以拿一本书。
对于所有 $0 \le i,j \le n-1$,桌子 $i$ 和桌子 $j$ 之间的距离正好是 $|j-i|$ 米。你的任务是,计算出 Aryan 重排好所有古书所走过的总距离的最小值。
实现细节
你需要实现下面的函数:
int64 minimum_walk(int[] p, int s)$p$ 是一个长度为 $n$ 的数组。初始阶段在桌子 $i$ 上的古书需要被 Aryan 移到桌子 $p[i]$ 上(对于所有 $0 \le i<n$)。
$s$ 是初始阶段 Aryan 所在桌子的编号,同时也是重排好所有古书之后他应该在的位置。
该函数要返回 Aryan 重排好所有古书所需走过的总距离的最小值(以米为单位)。
例子
minimum_walk([0, 2, 3, 1], 0)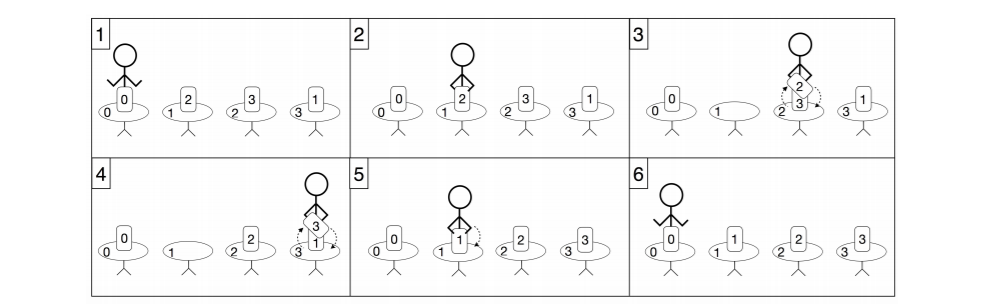
在这个例子中,$n=4$,在初始阶段Aryan位于桌子 $0$ 处。他按照如下步骤进行重排:
- 走到桌子 $1$ 处并且拿起桌上的书。这本书应该要被放到桌子 $2$ 上。
- 然后,他走到桌子 $2$ 处,并且把他手上的书和桌子上的书进行交换。现在他新拿到手上的书应该被放到桌子 $3$ 上。
- 然后,他走到桌子 $3$ 处,并且把他手上的书和桌子上的书进行交换。现在他新拿到手上的书应该被放到桌子 $1$ 上。
- 然后,他走到桌子 $1$ 处,并且把他手上的书放到桌子上。
- 最后,他回到桌子 $0$ 处。 注意,桌子 $0$ 上的书已经在正确的位置,即桌子 $0$ 上,因此 Aryan 不需要把它拿起来。在这个方案中,他的总行走距离是 $6$ 米。这是一个最优解;因此,函数应该返回 $6$。
限制
- $1 \le n \le 1\,000\,000$
- $0 \le s \le n-1$
- 数组 $p$ 包含 $n$ 个从 $0$ 到 $n-1$(含)的不同整数。
子任务
- ($12$ 分)$n \le 4$ 且 $s=0$
- ($10$ 分)$n \le 1000$ 且 $s=0$
- ($28$ 分)$s=0$
- ($20$ 分)$n \le 1000$
- ($30$ 分)没有附加任何限制
评测工具示例
评测工具示例将会读取如下格式的输入数据:
- 第 $1$ 行:$n~s$
- 第 $2$ 行:$p[0]~p[1]~\cdots~p[n-1]$
评测工具示例将输出一行,其中包括 minimum_walk 的返回值。
