题目描述
译自 CEOI 2019 Day1 T2「Dynamic Diameter」
你有一个 $n$ 个节点的树,每条边有边权,有 $q$ 次更新,每次修改一条边的边权,并询问树的直径。
本题强制在线。
输入格式
第一行输入三个正整数 $n, q, w$,表示节点数,询问数,以及一条边权值的上限。
接下来 $n - 1$ 行,其中第 $i$ 行三个整数 $a_i, b_i, c_i (1\le a_i, b_i \le n, 0\le c_i < w)$,表示链接节点 $a_i, b_i$ 的一条边权值为 $c_i$。
接下来 $q$ 行,每行两个整数 $d, e (0\le d < n - 1, 0 \le e < w)$,表示加密前的数据。
记 $\mathrm{last}$ 为上次询问的答案,第一次时为 $0$。解密后的数据为 $d' = (d + \mathrm{last}) \bmod (n - 1) + 1, e' = (e + \mathrm{last}) \bmod w$。表示将第 $d'$ 条边的权值修改为 $e'$。
输出格式
输出 $q$ 行,每行一个整数,表示修改后的直径。
样例 1
input
4 3 2000
1 2 100
2 3 1000
2 4 1000
2 1030
1 1020
1 890output
2030
2080
2050
这组样例如下图所示:
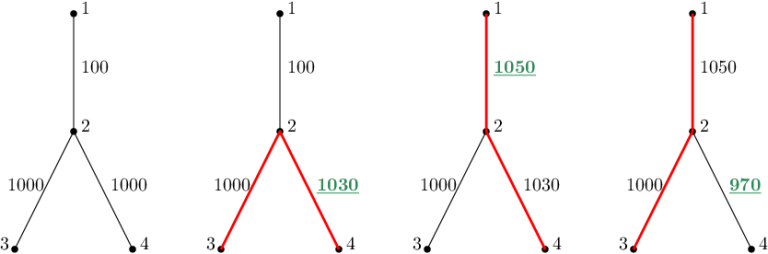
最左端图片是这棵树的初始状态,接下来的每张图表示在更新之后的情况。更改后的边权用绿色标记,直径用红色标记。
第一个询问更改了第三条边的边权,即 ${2,4}$ 的边权改为 $1030$。两点间最大距离为 $2030$,即 $3$ 到 $4$ 的距离。
因为第一个询问的答案为 $2030$,第二个询问为:
$$ d_2'=(1+2030)\bmod 3=0\ e_2'=(1020+2030)\bmod 2000=1050\ $$
因此边 ${1,2}$ 的边权改为 $1050$,这使得从 $1$ 到 $4$ 的距离最大,距离为 $2080$。
第三个询问为:
$$ d_3'=(1+2080)\bmod 3=2\ e_3'=(890+2080)\bmod 2000=970\ $$
因此边 ${2,4}$ 的边权改为 $970$,这使得从 $1$ 到 $3$ 的距离最大,距离为 $2050$。
样例 2
input
10 10 10000
1 9 1241
5 6 1630
10 5 1630
2 6 853
10 1 511
5 3 760
8 3 1076
4 10 1483
7 10 40
8 2051
5 6294
5 4168
7 1861
0 5244
6 5156
3 3001
8 5267
5 3102
8 3623output
6164
7812
8385
6737
6738
7205
6641
7062
6581
5155
数据范围与提示
对于 $100\%$ 的数据,保证 $2\le n \le 10^5, 1\le q\le 10^5, 1\le w \le 2\times 10^{13}$。
| 子任务编号 | $n, q$ | $w$ | 特殊限制 | 分值 |
|---|---|---|---|---|
| $1$ | $\le 10^2$ | $\le 10^4$ | $11$ | |
| $2$ | $\le 5\times 10^3$ | $\le 10^4$ | $13$ | |
| $3$ | $\le 10^5$ | $\le 10^4$ | 边的形式都为 $(1, i)$ | $7$ |
| $4$ | $\le 10^5$ | $\le 10^4$ | 边的形式都为 $(i, 2i)$ 或 $(i, 2i + 1)$ | $18$ |
| $5$ | $\le 10^5$ | $\le 2\times 10^{13}$ | 保证有一条直径经过 $1$ 号节点 | $24$ |
| $6$ | $\le 10^5$ | $\le 2\times 10^{13}$ | $27$ |
