题目描述

译自 COCI 2018/2019 Contest #3 T5「Praktični」

给一个有权无向图，我们称一个图是好的，当且仅当其每个简单环上的权值的异或和为 $0$。你一次操作可以选定图的一个边集以及一个数 $X$，操作是将该边集包含的边的权值都异或上 $X$。请求出至少需要多少次操作可以使给定的图变好。

输入格式

第一行输入两个正整数 $N,M$，表示图的点数和边数。

接下来 $M$ 行第 $i$ 行三个整数 $a_i, b_i, p_i$，表示第 $i$ 条边连接 $a_i, b_i$，权值为 $p_i$。保证图是联通的且没有重边。

输出格式

第一行输出一个整数 $K$，表示需要的最少操作次数。

接下来 $K$ 行每行第一个整数 $x$ 表示要异或的值，第二个整数 $B$ 表示选择的边集大小，接下来 $B$ 个整数第 $i$ 个 $E_i$ 表示所选取的第 $i$ 条边是输入中的第 $E_i$ 条，要求 $E_i$ 互不相同。请保证输入的数均不超过 $2 \times 10^9$。

样例 1

input

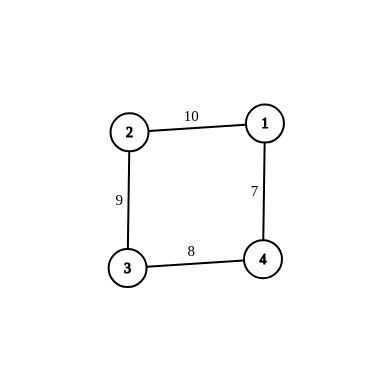
4 4
1 2 10
2 3 9
3 4 8
4 1 7

output

1
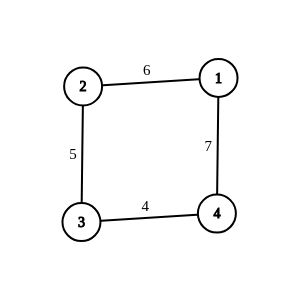
12 3 1 2 3

这是修改前的图

这是修改后的图

样例 2

input

2 1
1 2 3

output

0

这个图中没有简单环，因此不需要修改，显然满足条件。

样例 3

input

6 8
1 2 6
2 3 1
3 5 6
3 1 5
4 5 0
3 6 0
4 2 8
4 1 1

output

2
2 2 4 6
15 1 7

数据范围与提示

对于 $20\%$ 的数据，保证最优操作次数不超过 $1$。

对于另外 $40\%$ 的数据，保证输入的数都不超过 $10^6$。

对于 $100\%$ 的数据，保证：

• $1\le N, M \le 10^5$
• $1\le a_i, b_i \le N, a_i \neq b_i$
• $0\le p_i \le 10^9$