题目描述

法珞是个怕黑的女孩子。

傍晚了，法珞所参加的学术会议早已散会。黎瑟也下了课过来接法珞回火车站。

但是教学楼里突然断电了，法珞陷入了一片漆黑之中。

好在黎瑟已经到了教学楼的同一层。

然而由于教学楼的结构过于复杂，她们已经记不起教学楼的具体结构了。 黎瑟学校的教学楼每层的结构都非常工整。

形式化地说，教学楼的一层的平面结构可以画在二维平面上以 $(0,0)$ 为左上角顶点，$(n,m)$ 为右下角顶点的子矩形（记为 $(0,0) - (n,m)$ 的矩形）里，这个子矩形的四条边是教学楼的楼体(或者说是四段已知一定存在的墙)。

请注意，本题中的坐标系和普通的平面直角坐标系不同，$(0,0)$ 是左上角的顶点而 $(n,m)$ 是右下角的顶点。 $(i,j)$ 表示的是第 $i+1$ 行第 $j+1$ 列的顶点而不是横坐标为 $i$ 纵坐标为 $j$ 的顶点。

每一段墙（无法通过的部分）是一条端点为 $(i,j)$ 和 $(i',j')$ 的线段，记作 $(i,j) - (i',j')$ 的墙，其中 $|i-i'| + |j-j'| =1$ 且 $i,i'$ 是 $[0,n]$ 中的整数，$j,j'$ 是 $[0,m]$ 中的整数（每当我们之后使用 $(i,j) - (i',j')$ 的记法，我们都保证满足上述所有条件）。

法珞知道，对于这种结构，有一种办法可能让她找到黎瑟：法珞用左手扶住墙，手臂和墙面垂直，保持这个状态向前方走，在转弯处也保持左手一直扶墙的状态。按照这个方法她就可以环绕一周，可能与黎瑟相遇。

法珞一开始会给你需要维护的初始的（这层楼的）结构，之后会给你 $q$ 个请求。

• 操作 $1$：读入格式形如 $1\ x_0\ y_0\ x_1\ y_1$：法珞请求在当前结构里添加一段 $(x_0, y_0) - (x_1, y_1)$ 的墙，保证此前这段墙不存在且这段墙不在 $(0, 0)-(n, m)$ 的子矩形的四条边上。

• 操作 $2$：读入格式形如 $2\ x_0\ y_0\ x_1\ y_1$ 法珞请求在当前结构里删除一段 $(x_0,y_0) - (x_1,y_1)$ 的墙，保证此前这段墙存在且这段墙不在 $(0,0) - (n,m)$ 的子矩形的四条边上。

• 操作 $3$：读入形如 $3\ x_0\ y_0\ x_1\ y_1\ d_0\ x_2\ y_2\ x_3\ y_3\ d_1$：法珞当前在 $(x_0,y_0) - (x_1,y_1)$ 的墙的中点位置 $(\frac{x0+x1}{2},\frac{y_0 + y_1}{2})$，$d_0$ 是一个 $[0,1]$ 中的整数，用来描述法珞在墙的哪一侧，$d_0 = 0$ 代表法珞在墙的左方/上方，$d_0 = 1$ 代表右方/下方。黎瑟当前在 $(x_2,y_2) - (x_3,y_3)$ 的墙的中点位置 $(\frac{x2+x3}{2},\frac{y_2+y_3}{2})$。$d_1$ 的格式和 $d_0$ 相同。保证 $(x_0,y_0) - (x_1,y_1)$ 和 $(x_2,y_2) - (x_3,y_3)$) 这两段墙存在，且法珞和黎瑟的位置都落在 $(0,0) - (n,m)$ 的子矩形的内部。求法珞按照题目所述的方法找到黎瑟要走过多少长度（$(i,j) - (i',j')$ 这段墙的长度为 $1$，半段墙（由于起点和终点都在墙的中点处）的长度是 $\frac{1}{2}$）。

输入格式

输入共 $2n+q$ 行。

第一行三个整数 $n,m,q$，意义如题目中所示。

接下来的 $n$ 行，每行 $m-1$ 个 $[0,1]$ 中的整数，第 $i$ 行第 $j$ 列的整数为 $1$ 表示 $(i,j) - (i-1,j)$ 这一段有墙，为 $0$ 则表示 $(i,j) - (i - 1,j)$ 这一段没有墙。

接下来的 $n-1$ 行，每行 $m$ 个 $[0,1]$ 中的整数，第 $i$ 行第 $j$ 列的整数为 $1$ 表示 $(i,j) - (i,j-1)$ 这一段有墙，为 $0$ 则表示 $(i,j) - (i,j-1)$ 这一段没有墙。

接下来的 $q$ 行，每行一个操作，格式如题目中所示。

输出格式

对于每个询问，输出法珞按照题目所述的方法找到黎瑟要走过多少长度，如果法珞按照题目所述的方法无法找到黎瑟则输出 $\mathbf{-1}$。

样例

input

3 3 4
0 0
1 0
0 0
1 0 1
0 0 1
3 3 0 3 1 0 0 3 1 3 0
1 2 1 2 0
2 1 0 1 1
3 2 2 2 3 1 1 2 1 3 0

output

11
16

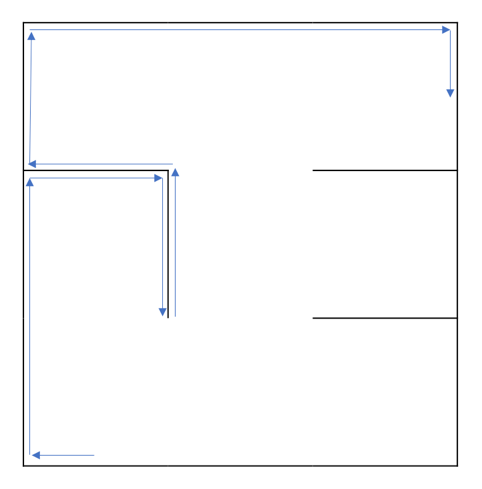
上图是样例输入中第一次询问的法珞的行走方案，在行走过程中法珞的左手必须贴住墙。

数据范围与提示

对于 $10\%$ 的数据，$5\le n, m\le 50, 1\le q\le 2\times 10^3$。

对于另外 $30\%$ 的数据，没有 $1$ 操作。

对于另外 $30\%$ 的数据，保证在任意时刻若法珞和黎瑟站在任意输入格式中合法的位置，法珞都可以和黎瑟相遇。

对于 $100\%$ 的数据，$5\le n, m\le 500, 1\le q\le 2\times 10^5$