题目描述
地灾军团的军师黑袍从潜伏在精灵高层的密探手中得知了神杖的情报,他对奥术宝石中蕴含的远古神秘力量十分感兴趣。他设计夺取了数块奥术宝石,并命令作为地灾军团首席科学家的你带领手下的研究人员全力破解。经过了一个月的艰苦尝试,你的研究团队终于破译了 「$2$」型奥术宝石和 「$3$」型奥术宝石的内部能量结构。
这两类结构有着一定的相似性,它们的内部具有 $k$ 个反应核心,「$2$」型奥术宝石的每个核心都可以看成是一个 $2 \times n$ 的网格,而 「$3$」型奥术宝石的每个核心都可以看成是一个 $3 \times n$ 的网格。(注意奥术宝石的 $k$ 和 $n$ 可能不同)当神力反应进行时,每个核心自动填充满神力颗粒。
形式化地描述,每个神力颗粒可以看成是一个 $1 \times 2$ 横置或竖置的方格,核心填满的定义为每个网格都恰好被一某个方格覆盖。若在两种填满反应核心的方案中存在一个方格放置的位置或方式不同,就认为方案不同。
如填满 $2×4$ 的网格有 $5$ 种不同的方案,填满 $3×2$ 的网格有 $3$ 种不同的方案。
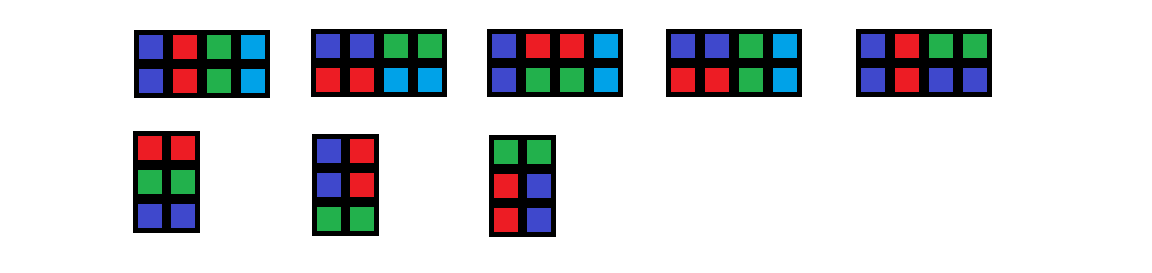
如果奥术宝石的 $k$ 个核心的填充方式互不相同,它们就会组合出强大的咒术。黑袍想知道对于某个宝石一共有多少种不同的咒术(对于两种咒术组合,如果第一种咒术中每个核心 $a$ 的填充方式都可以找到第二种咒术的某个核心 $b$,使得 $a$ 和 $b$ 的填充方式完全相同,则认为这两种咒术组合相同)。
对于宽度为 $n$、反应核心个数为 $k$ 的 「$2$」型奥术宝石,设不同的咒术为 $F(n,k)$;对于宽度为 $n$、反应核心个数为 $k$ 的「$3$」型奥术宝石,设不同的咒术为 $G(n,k)$。例如 $F(4,1) = 5,F(4,2) = 10,G(2,2) = 3$。
地灾军团的科技水平还不能精准测量反应核心的长度 $n$,只能确定出核心长度的大致范围 $[l,r]$。你需要计算出反应核心长度在此区间内的平均咒术数,即
$$\mathrm{ans2} = \frac{1}{r-l+1}\sum_{n=l}^{r} F(n,k)$$
$$\mathrm{ans3} = \frac{1}{r-l+1}\sum_{n=l}^{r} G(n,k)$$
设最终答案的形式为 $\frac{A}{B}$,输出 $A \times B^{-1} \bmod 998244353$ 的结果,其中 $B^{-1}$ 是 $B$ 在 $998244353$ 下的乘法逆元。
输入格式
第一行为两个正整数 $T$、$m$ ,表示数据组数和奥术宝石的类型(只可能为 $2$ 或 $3$ )。
接下来 $T$ 行每行三个正整数 $l,r,k$,表示核心长度的范围与核心数量。
输出格式
对于每组数据,若 $m=2$ 则输出 $\mathrm{ans2}$,$m=3$ 则输出 $\mathrm{ans3}$。
样例 1
input
5 2
2 4 2
1 10000 501
52501 233333333333 1
52501 233333333333 2
52501 233333333333 50output
665496240
218802505
745517510
133015204
910014966
样例 2
input
5 3
2 2 2
1 10000 501
52501 233333333333 1
52501 233333333333 2
52501 233333333333 50output
3
900767573
52671648
600503426
678428567
数据范围与提示
| 测试点 | $m=$ | $k$ | 特殊性质 |
|---|---|---|---|
| $1\sim 2$ | $2$ | $\le 501$ | $1\le l \le r \le 52501$ |
| $3$ | $2$ | $\le 501$ | $r - l + 1 \le 52501$ |
| $4$ | $2$ | $=1$ | |
| $5$ | $2$ | $=2$ | |
| $6\sim 7$ | $2$ | $\le 50$ | |
| $8\sim 10$ | $2$ | $\le 501$ | |
| $11\sim 12$ | $3$ | $\le 501$ | $1\le l \le r \le 52501$ |
| $13$ | $3$ | $\le 501$ | $r - l + 1 \le 52501$ |
| $14$ | $3$ | $=1$ | |
| $15$ | $3$ | $=2$ | |
| $16\sim 17$ | $3$ | $\le 50$ | |
| $18\sim 20$ | $3$ | $\le 501$ |
对于 $100\%$ 的数据,满足:
- $T=1$
- $1\le l\le r\le 10^{18}$
- $1\le k \le 501$
- $r - l + 1 \not \equiv 0 \pmod {998244353}$
时间限制根据 LOJ 评测机效率经过相应调整。
