题目描述
浮生有梦三千场
穷尽千里诗酒荒
徒把理想倾倒
不如早还乡温一壶风尘的酒
独饮往事迢迢
举杯轻思量
泪如潮青丝留他方——乌糟兽/愚青《旧词》
你已经解决了五个问题,不妨在这大树之下,吟唱旧词一首抒怀。最后的问题就是关于这棵树的,它的描述很简单。
给定一棵 $n$ 个点的有根树,节点标号 $1 \sim n$,$1$ 号节点为根。
给定常数 $k$。
给定 $Q$ 个询问,每次询问给定 $x,y$。
求:
$$\sum\limits_{i \le x} \text{depth}(\text{lca}(i,y))^k$$
$\text{lca}(x,y)$ 表示节点 $x$ 与节点 $y$ 在有根树上的最近公共祖先。
$\text{depth}(x)$ 表示节点 $x$ 的深度,根节点的深度为 $1$。
由于答案可能很大,你只需要输出答案模 $998244353$ 的结果。
输入格式
输入包含 $n+Q$ 行。
第 $1$ 行,三个正整数 $n,Q,k$。
第 $i = 2 \sim n$ 行,每行有一个正整数 $f_i(1 \le f_i \le n)$,表示编号为 $i$ 的节点的父亲节点的编号。
接下来 $Q$ 行,每行两个正整数 $x,y(1 \le x,y \le n)$,表示一次询问。
输出格式
输出包含 $Q$ 行,每行一个整数,表示答案模 $998244353$ 的结果。
样例
input
5 5 2
1
4
1
2
4 3
5 4
2 5
1 2
3 2output
15
11
5
1
6
输入的树:
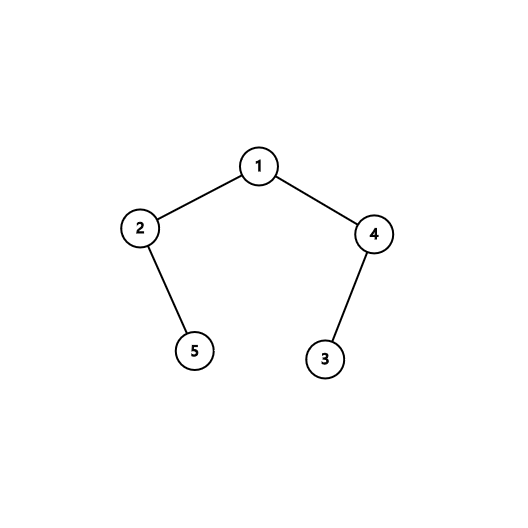
每个点的深度分别为 $1,2,3,2,3$。
第一个询问 $x = 4,y = 3$,容易求出:
$$\text{lca}(1, 3) = 1\ \text{lca}(2, 3) = 1\ \text{lca}(3, 3) = 3\ \text{lca}(4, 3) = 4$$
于是 $\text{depth}(1)^2+\text{depth}(1)^2+\text{depth}(3)^2+\text{depth}(4)^2 = 1+1+9+4 = 15$。
数据范围与提示
| 测试点编号 | $n$ 的规模 | $Q$ 的规模 | $k$ 的规模 | 约定 |
|---|---|---|---|---|
| $1$ | $n \le 2,000$ | $Q \le 2,000$ | $1 \le k \le 10^9$ | 无 |
| $2$ | $n \le 2,000$ | $Q \le 2,000$ | $1 \le k \le 10^9$ | 无 |
| $3$ | $n \le 2,000$ | $Q \le 2,000$ | $1 \le k \le 10^9$ | 无 |
| $4$ | $n \le 2,000$ | $Q \le 2,000$ | $1 \le k \le 10^9$ | 无 |
| $5$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 存在某个点,其深度为 $n$ |
| $6$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 存在某个点,其深度为 $n$ |
| $7$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 存在某个点,其深度为 $n$ |
| $8$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 存在某个点,其深度为 $n$ |
| $9$ | $n \le 50,000$ | $Q = n$ | $1 \le k \le 10^9$ | 对于第 $i$ 个询问,有 $x = i$ |
| $10$ | $n \le 50,000$ | $Q = n$ | $1 \le k \le 10^9$ | 对于第 $i$ 个询问,有 $x = i$ |
| $11$ | $n \le 50,000$ | $Q \le 50,000$ | $k = 1$ | 无 |
| $12$ | $n \le 50,000$ | $Q \le 50,000$ | $k = 1$ | 无 |
| $13$ | $n \le 50,000$ | $Q \le 50,000$ | $k = 2$ | 无 |
| $14$ | $n \le 50,000$ | $Q \le 50,000$ | $k = 2$ | 无 |
| $15$ | $n \le 50,000$ | $Q \le 50,000$ | $k = 3$ | 无 |
| $16$ | $n \le 50,000$ | $Q \le 50,000$ | $k = 3$ | 无 |
| $17$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 无 |
| $18$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 无 |
| $19$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 无 |
| $20$ | $n \le 50,000$ | $Q \le 50,000$ | $1 \le k \le 10^9$ | 无 |
