题目描述
九条可怜是一个喜欢数据结构的女孩子,在常见的数据结构中,可怜最喜欢的就是线段树。
线段树的核心是懒标记,下面是一个带懒标记的线段树的伪代码,其中 tag 数组为懒标记:

其中函数 $\texttt{Lson}(\text{Node})$ 表示 $\text{Node}$ 的左儿子,$\texttt{Rson}(\text{Node})$ 表示 $\text{Node}$ 的右儿子。
现在可怜手上有一棵 $[1, n]$ 上的线段树,编号为 $1$。这棵线段树上的所有节点的 tag 均为 $0$。接下来可怜进行了 $m$ 次操作,操作有两种:
- $1\ l\ r$,假设可怜当前手上有 $t$ 棵线段树,可怜会把每棵线段树复制两份(
tag数组也一起复制),原先编号为 $i$ 的线段树复制得到的两棵编号为 $2i − 1$ 与 $2i$,在复制结束后,可怜手上一共有 $2t$ 棵线段树。接着,可怜会对所有编号为奇数的线段树进行一次 $\texttt{Modify}(\text{root}, 1, n, l, r)$。 - $2$,可怜定义一棵线段树的权值为它上面有多少个节点
tag为 $1$。可怜想要知道她手上所有线段树的权值和是多少。
输入格式
第一行输入两个整数 $n, m$ 表示初始区间长度和操作个数。
接下来 $m$ 行每行描述一个操作,输入保证 $1 \le l \le r \le n$。
输出格式
对于每次询问,输出一行一个整数表示答案,答案可能很大,对 $998244353$ 取模后输出即可。
样例
input
5 5
2
1 1 3
2
1 3 5
2output
0
1
6
$[1, 5]$ 上的线段树如下图所示:
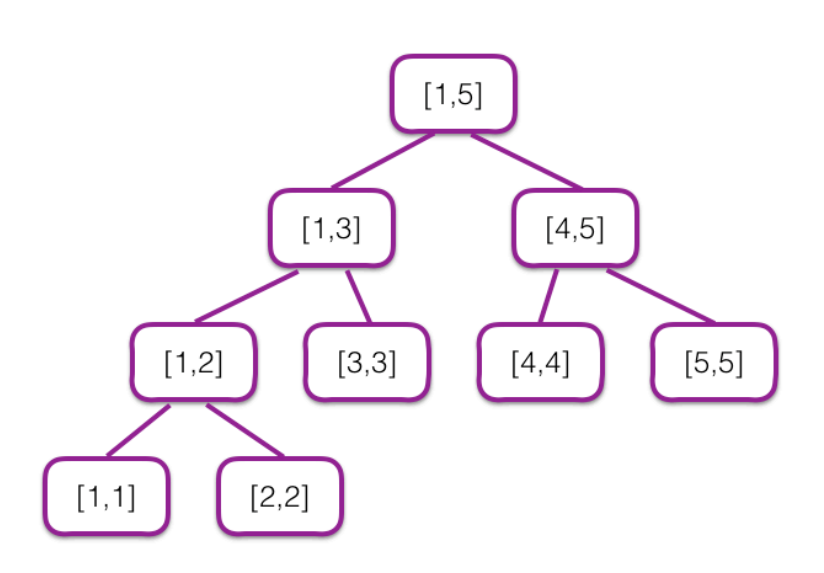
在第一次询问时,可怜手上有一棵线段树,它所有点上都没有标记,因此答案为 $0$。
在第二次询问时,可怜手上有两棵线段树,按照编号,它们的标记情况为:
- 点 $[1, 3]$ 上有标记,权值为 $1$。
- 没有点有标记,权值为 $0$。
因此答案为 $1$。
在第三次询问时,可怜手上有四棵线段树,按照编号,它们的标记情况为:
- 点 $[1, 2], [3, 3], [4, 5]$ 上有标记,权值为 $3$。
- 点 $[1, 3]$ 上有标记,权值为 $1$。
- 点 $[3, 3], [4, 5]$ 上有标记,权值为 $2$。
- 没有点有标记,权值为 $0$。
因此答案为 $6$。
数据范围与提示
| 测试点 | $n$ | $m$ | 其他约定 |
|---|---|---|---|
| $1$ | $\le 10^3$ | $\le 10$ | 无 |
| $2$ | $\le 10^3$ | $\le 10$ | 无 |
| $3$ | $\le 10^3$ | $\le 10^3$ | 无 |
| $4$ | $\le 10^3$ | $\le 10^3$ | 无 |
| $5$ | $\le 10^5$ | $\le 10^5$ | 询问只有一个 |
| $6$ | $\le 10^5$ | $\le 10^5$ | 询问只有一个 |
| $7$ | $\le 10^5$ | $\le 10^5$ | 询问只有一个 |
| $8$ | $\le 10^5$ | $\le 10^5$ | 无 |
| $9$ | $\le 10^5$ | $\le 10^5$ | 无 |
| $10$ | $\le 10^5$ | $\le 10^5$ | 无 |
对于 $100\%$ 的数据,$1 \le l \le r \le n$。
