题目描述
译自 JOI 2019 Final T4「コイン集め / Coin Collecting」
JOI 先生的收藏室里有一张巨大的桌子,上面有许多稀有的硬币。为了清理桌子,他要重新摆放硬币。
桌面可视为 $(2\times 10^9+1) \times (2\times 10^9+1)$ 的网格。网格上往下数第 $i$ 行($-10^9 \le i \le 10^9$),左往右数第 $j$ 列($-10^9 \le j \le 10^9$)的格子坐标记为 $(i, j)$ 。
JOI 先生有 $2N$ 枚硬币。初始时,第 $i$ 枚 $(1 \le i \le 2N)$ 硬币被放在坐标为 $(X_i, Y_i)$ 的格子里。JOI 先生的目标是在每个满足 $1 \le x \le N, 1 \le y \le 2$ 的格子 $(x,y)$ 上恰好放一枚硬币。为了不损坏硬币,他能做的唯一一个操作是钦定一枚硬币然后将其移动到相邻的一个格子中(我们说两个格子相邻,当且仅当这两个格子有公共边)。在移动硬币的过程中,允许两个硬币处在同一个格子中。JOI 先生希望通过尽量少的操作次数完成目标。
现在给出硬币的数量和初始时所在的位置,编写一个程序,计算完成 JOI 先生目标所需的最少操作次数。
输入格式
从标准输入中读取数据。
第一行一个整数 $N$。
接下来 $2N$ 行,第 $i$ 行为两个整数 $X_i$ 和 $Y_i$。
输出格式
输出数据到标准输出中。
输出一行一个整数,表示完成目标所需的最少操作次数。
样例 1
input
3
0 0
0 4
4 0
2 1
2 5
-1 1output
15
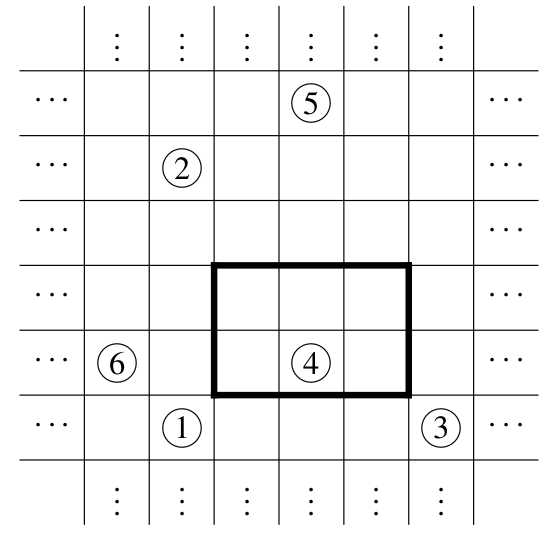
一种合法的移动方案是:
- 一号硬币: $(0, 0) \rightarrow (1, 0) \rightarrow (1, 1) \rightarrow (1, 2)$
- 二号硬币: $(0, 4) \rightarrow (1, 4) \rightarrow (1, 3) \rightarrow (2, 3) \rightarrow (3, 3) \rightarrow (3, 2)$
- 三号硬币: $(4, 0) \rightarrow (4, 1) \rightarrow (3, 1)$
- 五号硬币: $(2, 5) \rightarrow (2, 4) \rightarrow (2, 3) \rightarrow (2, 2)$
- 六号硬币: $(-1, 1) \rightarrow (0, 1) \rightarrow (1, 1)$
可以证明 JOI 先生不能用少于 15 次移动完成目标。
样例 2
input
4
2 1
2 1
2 1
3 1
3 1
3 1
3 1
3 1output
9
样例 3
input
5
1000000000 1000000000
-1000000000 1000000000
-1000000000 -1000000000
1000000000 -1000000000
-1 -5
-2 2
2 8
4 7
-2 5
7 3output
8000000029
数据范围与提示
| Subtask # | 分值 | $N$ |
|---|---|---|
| 1 | 8 | $N \le 10$ |
| 2 | 29 | $N \le 1000$ |
| 3 | 63 | $N \le 10^5$ |
对于所有输入数据,有 $1 \le N \le 10^5, -10^9 \le X_i, Y_i \le 10^9$。
