题目描述
译自 JOISC 2015 Day4 T3「防壁」,感谢 PoPoQQQ 提供翻译。
你入手了一款 JOI 社发售的游戏。你对这款游戏十分上手,每天玩得不亦乐乎。
某一天,玩家之中出现了一个叫做「镭射」的关卡。这个关卡十分的难,连老司机玩家也只有很低的概率才能通过。正在三番五次挑战这个关卡的你,很快判断出通过的可能性是存在的,并考虑写一个程序来计算出对策。
镭射关卡在一个配置有 $N$ 个防壁的地形上进行。地形为长方形,分成了一些 $1\times 1$ 的正方形区域。每个区域可以用两个非负整数 $(x,y)$ 表示,左下角的区域为 $(0,0)$,$(x,y)$ 表示 $(0,0)$ 往右数 $x$ 个区域,再往上数 $y$ 个区域的位置。
关卡开始后,敌人会出现并顺次进行 $M$ 轮攻击。第 $j$ 次攻击时,敌人将会从区域 $(P_j,N+1)$ 向区域 $(P_j,0)$ 进行直线镭射射击。
每个防壁放在 $y$ 坐标相同的一些连续的区域中。防壁 $i(1\le i\le N)$ 是左右长度为 $B_i-A_i+1$,上下宽度为 $1$ 的长方形,初始位置为 $(A_i,i)$ 到 $(B_i,i)$ 的所有区域。在敌人开始攻击之前以及两次攻击的间隙,你可以任意次地左右移动防壁。一次移动可以让防壁向右移动一个区域,或者向左移动一个区域。
镭射在穿过一个防壁后威力会减少。现在为了将镭射的威力最小化,需要移动防壁使得镭射能穿过所有的防壁。你想让移动防壁的次数尽量少。
现在给出关卡开始时每个防壁的位置,以及每个敌人的攻击位置,为了让每一发镭射都穿过所有的防壁,请你输出每个防壁移动次数的最小值。
输入格式
第一行两个空格分隔的整数 $N,M$,表示这个关卡有 $N$ 个防壁,敌人将会进行 $M$ 轮攻击。
接下来 $N$ 行,第 $i$ 行有两个空格分隔的整数 $A_i,B_i$,表示关卡开始时防壁 $i$ 被放置在 $(A_i,i)$ 到 $(B_i,i)$ 的所有区域的位置上。
接下来 $M$ 行,第 $j$ 行有一个整数 $P_j$,表示第 $j$ 次攻击时,敌人从 $(P_j,N+1)$ 向 $(P_j,0)$ 进行直线镭射射击。
输出格式
输出 $N$ 行,第 $i$ 行表示防壁 $i$ 的移动次数的最小值。
样例 1
input
4 4
0 3
4 4
2 7
8 11
6
4
3
8output
5
10
1
7
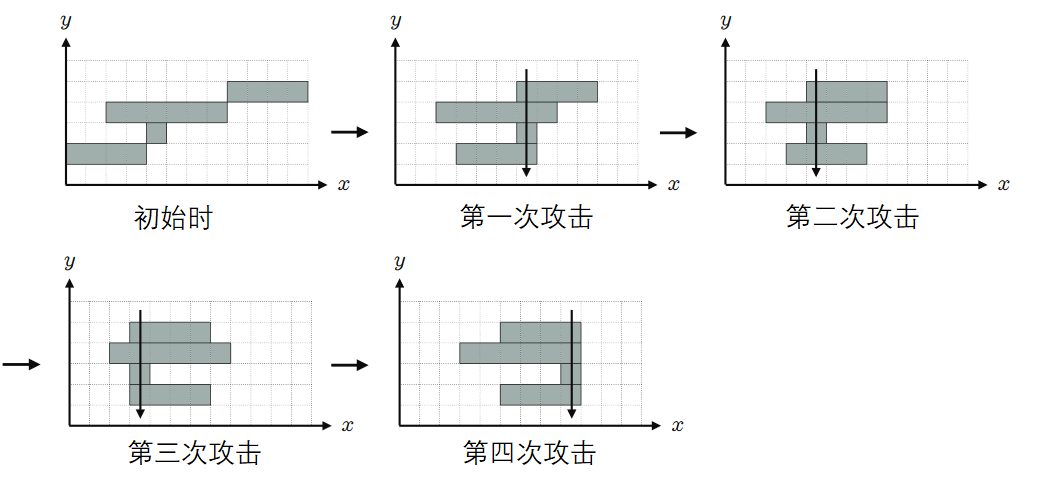
在这个输入中,使防壁的移动次数最少的移动方法之一如下:
- 对于第一轮攻击,防壁 $1$ 向右移动 $3$ 次,防壁 $2$ 向右移动 $2$ 次,防壁 $3$ 不动,防壁 $4$ 向左移动 $2$ 次;
- 对于第二轮攻击,防壁 $1$ 不动,防壁 $2$ 向左移动 $2$ 次,防壁 $3$ 不动,防壁 $4$ 向左移动 $2$ 次;
- 对于第三轮攻击,防壁 $1$ 不动,防壁 $2$ 向左移动 $1$ 次,防壁 $3$ 不动,防壁 $4$ 向左移动 $1$ 次;
- 对于第四轮攻击,防壁 $1$ 向右移动 $2$ 次,防壁 $2$ 向右移动 $5$ 次,防壁 $3$ 向右移动 $1$ 次,防壁 $4$ 向右移动 $2$ 次;
在这种移动方式中,防壁 $1$ 移动了 $5$ 次,防壁 $2$ 移动了 $10$ 次,防壁 $3$ 移动了 $1$ 次,防壁 $4$ 移动了 $7$ 次。
样例 2
input
7 11
12 39
22 23
5 38
6 47
10 43
0 50
18 46
38
19
15
1
12
29
29
0
6
40
6output
34
178
13
6
18
0
36
数据范围与提示
对于全部数据,满足 $1\le N,M\le 2\times 10^5,0\le A_i\le B_i\le 10^9,0\le P_j\le 10^9$。
本题共有 $3$ 个子任务。每个子任务的分数和附加限制如下:
| Subtask | 附加限制 | 分数 |
|---|---|---|
| $1$ | $N=1$ | $10$ |
| $2$ | $A_i=0$ | $45$ |
| $3$ | 无附加限制 | $45$ |
