题目描述
有 $n$ 个人坐在地上围成一个大圆,面朝圆心。游戏开始前将其中一个人编为 $1$ 号,$1$ 号右手边的人编为 $2$ 号,$2$ 号右手边的人编为 $3$ 号,以此类推,并在 $1$ 号脚下画一个正方形,$2\sim n$ 号脚下画一个圆。
游戏进行 $k$ 轮。第 $i$ 轮站在正方形里的人先喊一声「是我」。然后和他右手边的人交换位置 $p_k$ 次,$p_k$ 表示第 $k$ 个质数。下图展示了 $n=5,k=3$ 时每一轮的情况:
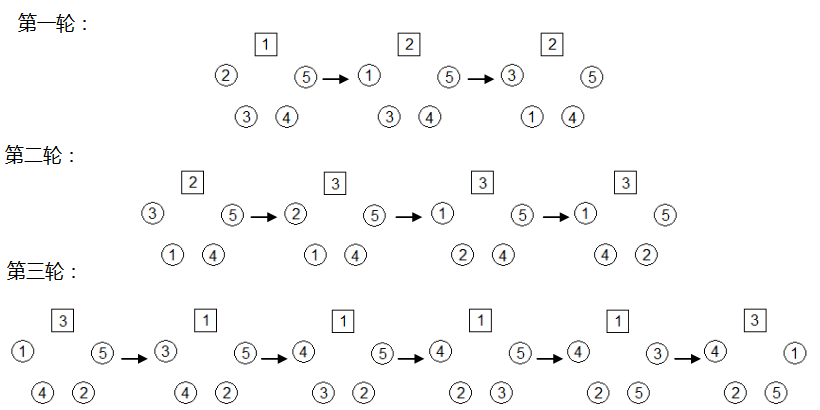
给定 $n,k,a$,求出 $k$ 轮结束后 $a$ 的左右邻居的编号。
输入格式
输入只有一行,包含三个整数 $n,k,a$。
输出格式
输出两个整数,分别表示 $k$ 轮后 $a$ 的右边和左边的人的编号。
样例 1
input
5 3 1output
3 5
样例 2
input
5 3 2output
5 4
样例 3
input
5 4 5output
3 2
数据范围与提示
对于 $25\%$ 的数据,$3\le n\le 10^3,1\le k\le 10^3$;
对于 $50\%$ 的数据,$3\le n\le 10^3,1\le k\le 5\times 10^4$;
对于 $75\%$ 的数据,$3\le n\le 5\times 10^4,1\le k\le 5\times 10^4$;
对于全部数据,$3\le n\le 5\times 10^6,1\le k\le 5\times 10^5,1\le a\le n$。
