题目描述
RMT 地铁交通运行着一个不寻常的地铁系统。有 $N$ 个地铁站,从 $1$ 到 $N$ 编号。有 $M$ 条地铁线路,从 $1$ 到 $M$ 编号,每个地铁站只属于一条线路且每条线路至少经过一个地铁站。整个地铁网络呈圆形。也就是说,如果有一个编号为 $S$ 的地铁站,那么与它同一线路的下一个地铁站是下一个编号比它大的地铁站。除非 $S$ 是同线路中编号最大的地铁站,在这种情况下,它的下一个地铁站是同一线路中编号最小的地铁站。
RMT 正在以志愿者对他们的系统进行负载测试。测试从每一站以一列地铁列车开始,且对于每一个 $i$,会有 $A_i$ 个志愿者在第 $i$ 站的测试列车上。在整个测试期间,志愿者不会离开对应的列车。
测试过程中,RMT 会进行 $Q$ 个操作,每个操作只有两种可能:一种是询问第 $l$ 站到第 $r$ 站地铁上的志愿者人数;或是在线路 $x$ 运行所有的地铁。当有一列地铁在 $x$ 线路运行,它会前往线路中的下一站。
你是 RMT 的铁杆骨灰级粉丝,所以你自愿协助他们进行操作并告诉他们操作的结果。
输入格式
第一行,三个整数,$N,M$ 和 $Q(1 \le M \le N \le 150\ 000;1 \le Q \le 150\ 000)$。
第二行,$N$ 个整数 $L_1,L_2,\dots,L_N$,表示每个地铁站所属线路的编号。
第三行,$N$ 个整数 $A_1,A_2,\dots,A_N$,表示每个地铁站起始时刻的志愿者人数。
以下 $Q$ 行,每行只有以下其中一种形态:
-
1 l r,表示一个询问 $(1 \le l \le r \le N)$。 2 x,表示 RMT 会在 $x$ 线路运行 $(1 \le x \le M)$。
输出格式
对于每个询问,输出一行,表示询问的答案。
样例 1
input
5 2 5
1 2 1 2 2
1 2 3 4 5
1 1 5
2 1
1 3 5
2 2
1 1 3output
15
10
9
地铁系统如下图所示,地铁站编号为 $1$ 到 $5$,由编号为 $1$ 或 $2$ 的线路连接:
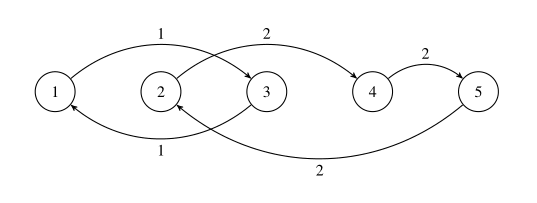
开始时,每个地铁站的志愿者人数为 ${1,2,3,4,5}$。
第一个询问的答案为 $1+2+3+4+5=15$。
线路 $1$ 被运行之后,每个地铁站的志愿者人数为 ${3,2,1,4,5}$。
第二个询问的答案为 $1+4+5=10$。
线路 $2$ 被运行之后,每个地铁站的志愿者人数为 ${3,5,1,2,4}$。
第三个询问的答案为 $3+5+1=9$。
样例 2
input
3 1 7
1 1 1
114 101 109
1 1 1
2 1
1 1 1
2 1
1 1 1
2 1
1 1 1output
114
109
101
114
地铁系统如下图所示,地铁站编号为 $1$ 到 $3$,只有线路 $1$ 连接:
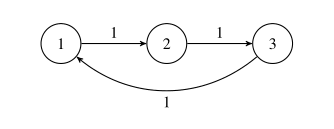
第一次询问之前,每个地铁站的志愿者人数为 ${114,101,109}$。
第二次询问之前,每个地铁站的志愿者人数为 ${109,114,101}$。
第三次询问之前,每个地铁站的志愿者人数为 ${101,109,114}$。
第四次询问之前,每个地铁站的志愿者人数为 ${114,101,109}$。
数据范围与提示
对于 $\frac2{15}$ 的数据,$N \le 1\ 000,Q \le 1\ 000$。
对于另外 $\frac2{15}$ 的数据,$L_i \le L{i+1}(1 \le i < N)$。
对于另外 $\frac3{15}$ 的数据,$M \le 200$。
对于另外 $\frac3{15}$ 的数据,每条线路的地铁数量都不超过 $200$。
