题目描述
在 Byteland 的首都,有一个以围墙包裹的矩形公园,其中以圆形表示游客和树。
公园里有四个入口,分别在四个角落($1, 2, 3, 4$ 分别对应左下、右下、左上、右上)。游客只能从入口进出。
游客可以在他们与公园的两邻边相切的时候进出对应的出口。游客可以在公园里自由活动但不允许与树重叠。
你的任务是为每个游客计算,给定他们进入公园的入口,他们可以从哪个入口离开公园。
输入格式
第一行包含两个整数 $n$ 和 $m$,分别为树的个数和游客的个数。
第二行包含两个整数 $w$ 和 $h$,公园的左下角在 $(0,0)$,右上角在 $(w,h)$。
接下来 $n$ 行,每行三个整数 $x,y$ 和 $r$,表示有一棵圆心在 $(x,y)$ 且半径为 $r$ 的树。保证树与树之间不会互相重叠。
接下来 $m$ 行,每行两个整数 $r$ 和 $e$,表示有一个半径为 $r$ 的游客从入口 $e$ 进入。
此外,保证没有树会与每个角落的一个大小为 $2k^2$ 的方形区域重叠,$k$ 表示最大的游客半径。
输出格式
对于每个游客,输出没有空格的一行,表示该游客可以从这几个入口离开,按照升序排列。
样例
input
5 3
16 11
11 8 1
6 10 1
7 3 2
10 4 1
15 5 1
1 1
2 2
2 1output
1234
2
14
数据范围与提示
两个物体有重叠定义为它们不止一个公共点。
下图展示了每个游客的入口和可能的路线:
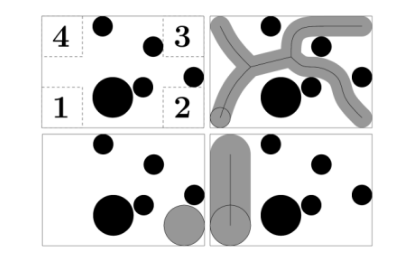
对于每个子任务,$4k \leq w,h \leq 10^9$,$k$表示最大的游客半径。
| 子任务 | 分数 | 数据范围 |
|---|---|---|
| 1 | 27 | $1 \leq n \leq 2000,m=1$ |
| 2 | 31 | $1 \leq n \leq 200,1 \leq m \leq 10^5$ |
| 3 | 42 | $1 \leq n \leq 2000,1 \leq m \leq 10^5$ |
