题目描述
本题的目标是求一个点数无穷的无向图的桥。 这个无向图具有如下性质:
- 这个图是一个连通图;
- 这个图的所有节点分为若干层,分别是第 $1$ 层、第 $2$ 层、第 $3$ 层……共有无穷层, 每层共有 $n$ 个节点。为了描述方便, 以下用 $(i, x)$ 表示第 $i$ 层的 $x$ 号节点;
- 同一层内的节点可以相互连边, 相邻两层的节点之间可以相互连边,除此之外,其他节点之间不能相互连边;
- 如果 $(i, x)$ 与 $(i, y)$ 之间有一条权值为 $d$ 的边,那么 $(j, x)$ 与 $(j, y)$ 之间也有一条边,它的权值为 $0.9^{j-i}d$,其中 $j$ 为任意正整数;
- 如果 $(i, x)$ 与 $(i + 1, y)$ 之间有一条权值为 $d$ 的边,那么 $(j, x)$ 与 $(j + 1, y)$ 之间也有一条边,它的权值为 $0.9^{j-i}d$,其中 $j$ 为任意正整数。
如下所示的无向图就符合上面的所有性质。
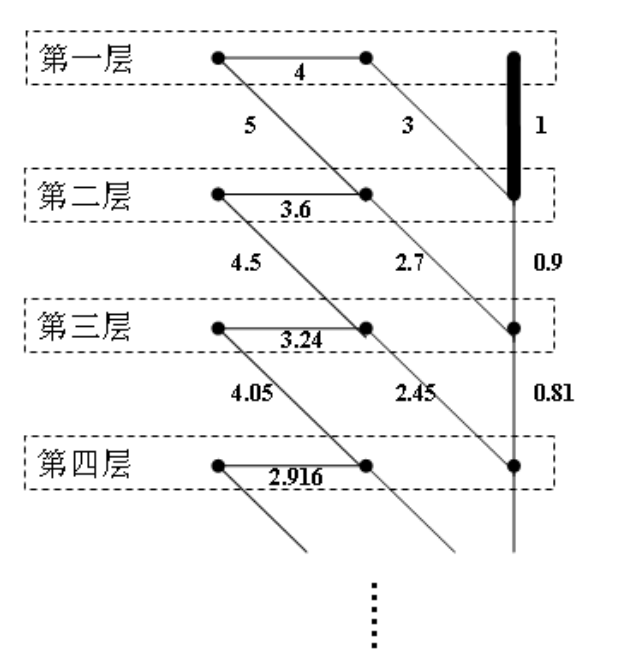
一个点数无穷的无向图是连通的,当且仅当对于图中的任意两个节点都存在一条路径将它们连接起来。而一条边是桥,当且仅当这条边被删去后整个图不连通。
请你编写程序读入这个点数无穷的连通图,求出其中所有桥的权值之和。例如,在上图中,粗线所示的边就是该图唯一的桥,因此上图中桥的权值之和为 $1$。
输入格式
第一行包括三个由空格隔开的非负整数 $n, m_1, m_2$;
从第二行到第 $m_1 + 1$ 行,每行有三个正整数 $x, y, d$,表示 $(1, x)$ 与 $(1, y)$ 之间有一条权值为 $d$ 的边;
从第 $m_1 + 2$ 行到第 $m_1 + m_2 + 1$ 行,每行有三个正整数 $x, y, d$,表示 $(1, x)$ 与 $(2, y)$ 之间有一条权值为 $d$ 的边。
每行的三个整数之间都用一个空格隔开。图中两个点 $x$ 和 $y$ 之间可能有多于 $1$ 条边连接,一条边连接的两个节点可能相同。
输出格式
只有一行,包含一个实数,即所有桥的权值之和,四舍五入保留两位小数。
样例 1
input
3 1 3
1 2 4
1 2 5
2 3 3
3 3 1output
1.00
这就是问题描述中所举的例子。
样例 2
input
1 1 1
1 1 100
1 1 1output
10.00
数据范围与提示
| 测试点编号 | $n$ | $m_1$ | $m_2$ |
|---|---|---|---|
| $1$ | $\le 10$ | $\le 50$ | $\le 50$ |
| $2$ | $\le 10^4$ | $\le 4\times 10^4$ | $\le 4\times 10^4$ |
| $3$ | $\le 3\times 10^5$ | $\le 5\times 10^5$ | $=1$ |
| $4\sim 7$ | $\le 3\times 10^5$ | $\le 5\times 10^5$ | $\le 500$ |
| $8\sim 10$ | $\le 3\times 10^5$ | $\le 5\times 10^5$ | $\le 5\times 10^5$ |
对于全部数据,$d\le 100$。
