题目描述
题目译自 JOISC 2016 Day3 T3 「電報」
给出 $N$ 个点,每个点的出度均为 $1$,给出这 $N$ 个点初始指向的点 $A_i$,和改变这个点指向的目标所需要的价值 $C_i$。
求让所有点强连通的最小花费。
输入格式
第一行输入一个数 $N$ 表示点的个数。
之后的 $N$ 行每行两个数 $A_i$ $C_i$ 表示第 $i$ 个点指向第 $A_i$ 个点,更改该点指向的点花费为 $C_i$。
输出格式
共一行,为让所有点强连通的最小花费。
样例 1
input
4
2 2
1 4
1 3
3 1output
4
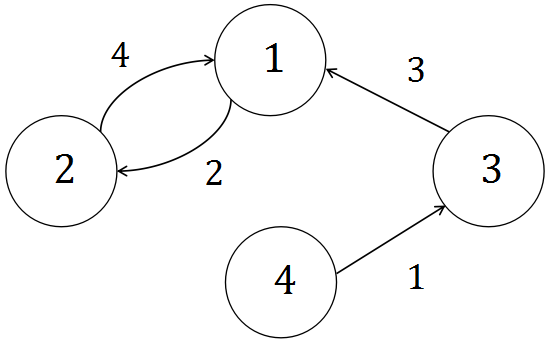
很显然,把 $2 \rightarrow 1$ 的这条边改成 $2 \rightarrow 4$(花费 4)的情况下构成强连通分量花费最小。
样例 2
input
4
2 2
1 6
1 3
3 1output
5
很显然把 $1 \rightarrow 2$ 的这条边改成 $1 \rightarrow 4$ 花费 2,把 $3 \rightarrow 1$ 的这条边改成 $3 \rightarrow 2$ 花费 3 的情况下构成强连通分量花费最小,总花费为 5。
样例 3
input
4
2 2
1 3
4 2
3 3output
4
样例 4
input
3
2 1
3 1
1 1output
0
数据范围与提示
对于全部的数据,$1 \leq N \leq 10^{5}$ ,$1 \leq A_i \leq N$ , $A_i \neq i$ , $1 \leq C_i \leq 10^{9} $。
具体子任务限制及得分情况如下表:
| Subtask | 限制 | 分数 |
|---|---|---|
| $1$ | $1 \leq N \leq 10 $ | $10$ |
| $2$ | $1 \leq N \leq 15$ | $30$ |
| $3$ | $1 \leq N \leq 3000$ | $30$ |
| $4$ | 无追加限制 | $30$ |
