题目描述
题目译自 JOISC 2016 Day1 T3 「ソリティア」
JOI 君有一个棋盘,棋盘上有 $N$ 行 $3$ 列 的格子。JOI 君有若干棋子,并想用它们来玩一个游戏。初始状态棋盘上至少有一个棋子,也至少有一个空位。
游戏的目标是:在还没有放棋子的格子上依次放棋子,并填满整个棋盘。在某个格子上放置棋子必须满足以下条件之一:
- 这个格子的上下一格都放有棋子;
- 这个格子的左右一格都放有棋子。
JOI 君想知道有多少种从初始状态开始,并达到游戏目标的方案,这个答案可能会非常大。请你帮 JOI 君算出这个答案,并对 $10^9+7$ 取模。
输入格式
第一行有一个整数 $N$ ,表示棋盘的大小为纵向 $3$ 格,横向 $N$ 格。
接下来的三行均为仅由 o 和 x 组成的字符串。这三行中第 $i$ 行的第 $j$ 个字符表示棋盘中从上到下第 $i$ 行,从左到右第 $j$ 个棋子的状态。其中 o 表示开始时有棋子被放置,x 表示开始时这个位置为没有放置着棋子。
输出格式
一个整数,表示符合条件的方案个数。
样例 1
input
3
oxo
xxo
oxooutput
14
对于样例 $1$,游戏的初始状态如下图所示(用 ◯ 表示有棋子放置):
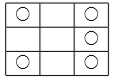
以下是所有可以从初始状态达到最终状态的方案(序号为放棋子的顺序):
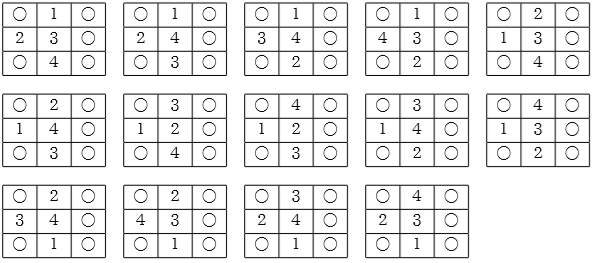
一共有 $14$ 种方案,因此输出 $14$。
样例 2
input
10
ooxooxoxoo
xooxxxoxxx
oxoxoooooooutput
149022720
样例 $2$ 满足所有子任务的限制。
样例 3
input
10
ooxoxxoxoo
oxxxxxoxxx
oxooxoxoxooutput
0
没有可以达到最终状态的方案。
样例 4
input
20
oxooxoxooxoxooxoxoxo
oxxxoxoxxxooxxxxxoox
oxooxoxooxooxooxoxoooutput
228518545
数据范围与提示
对于所有数据,满足 $1 \le N \le 2000$。
| Subtask | 分值 | $N$ | 其他 |
|---|---|---|---|
| $1$ | $10$ | $N\le30$ | 初始时空格子少于 $16$ 个。 |
| $2$ | $12$ | $N\le2000$ | 初始时对于任意一个空格子,其上下左右相邻的空格子数不超过 $2$ 个。 |
| $3$ | $20$ | $N\le30$ | 初始时没有连续 $3$ 个空格子并成一列 |
| $4$ | $38$ | $N\le300$ | 无 |
| $5$ | $20$ | $N\le2000$ | 无 |
