题目描述
有一个装球机器,构造可以看作是一棵树。有下面两种操作:
从根放入一个球,只要下方有空位,球会沿着树滚下。如果同时有多个点可以走,那么会选择编号最小的节点所在路径的方向。比如依次在树根 $4$ 放 $2$ 个球,第一个球会落到 $1$,第二个会落到 $3$:
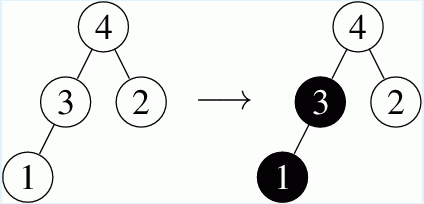
从某个位置拿走一个球,那么它上方的球会落下来。比如依次拿走 $5, 7, 8$ 三个球:

输入格式
第一行:球的个数 $N$,操作个数 $Q(N, Q \le 10^5)$
下面 $N$ 行:第 $i$ 个节点的父亲。如果是根,则为 $0$
接下来 $Q$ 行:op num
- $op = 1$:在根放入
num个球 - $op = 2$:拿走在位置
num的球
输出格式
保证输入合法
- $op = 1$:输出最后一个球落到了哪里
- $op = 2$:输出拿走那个球后有多少个球会掉下来
样例
input
8 4
0
1
2
2
3
3
4
6
1 8
2 5
2 7
2 8output
1
3
2
2
数据范围与提示
对于 $25\%$ 的数据,每个节点有 $0$ 或 $2$ 个儿子,且所有叶子节点到根的距离相同。
对于另外 $30\%$ 的数据,操作 $2$ 不会使球落下。
对于另外 $40\%$ 的数据,只有一个操作 $1$,并且是第一个操作。
对于所有数据,$N, Q \le 100\ 000$.
翻译来自 abcdabcd987。
