题目描述
译自 JOI Open 2017 T2 「ブルドーザー / Bulldozer」
平面上有 $N$ 个点,点 $i\:(1≤i≤N)$ 位于 $(X_i, Y_i)$,点 $i\:(1≤i≤N)$ 的权值为非零整数 $W_i$(可能为负数)。
在平面上画两条平行线,所得的总价值为平行线之间(压线也算)所有点的权值之和。求总价值至多不超过多少。
输入格式
第一行包含一个整数 $N$。
在接下来的 $N$ 行中,第 $i$ 行包含三个用空格分隔的整数 $X_i,Y_i,W_i$。
输出格式
一行,一个整数,表示最大总价值。
样例 1
input
5
-5 5 -2
2 5 10
1 4 -2
4 -5 4
-2 2 7output
19
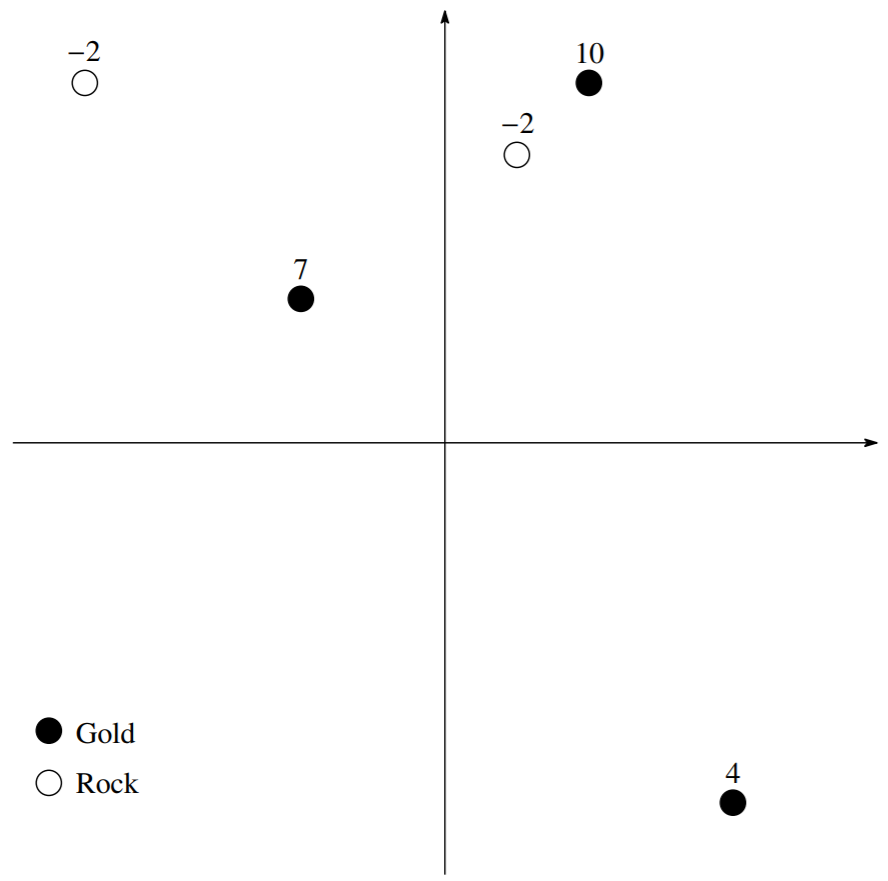
选择点 $2, 3, 4, 5$。
样例 2
input
6
0 0 6
1 0 -2
2 0 8
0 1 -2
1 1 5
2 1 -2output
15
注意,点 $1,2,3$ 共线。点 $4,5,6$ 共线。
样例 3
input
5
0 0 2
4 0 2
3 2 -1
1 2 2
1 1 -1output
5
这组样例中没有三点共线。选择的平行线一条过点 $1,2$,另一条过点 $3,4$。
样例 4
input
2
0 0 -1
1 0 -1output
0
数据范围与提示
所有输入数据都满足以下条件。
$1≤N≤2000, |X_i|,|Y_i|≤10^9,1 ≤|W_i|≤10^9(1≤i≤N)$ 。$(X_i,Y_i)≠(X_j,Y_j)\:(1≤i<j≤N)$ 。
| 子任务 | 分值 | $N≤100$ | 无三点共线 | 设 $L$ 是在平面上通过两个不同点的一条线,$L'$ 是在平面上另一条通过两个不同点的线,那么 $L$ 和 $L'$ 不相互平行 | 其他条件 |
|---|---|---|---|---|---|
| $1$ | $5$ | √ | × | × | 所有点都在 $x$ 轴上 |
| $2$ | $20$ | √ | √ | √ | 无 |
| $3$ | $35$ | × | √ | √ | 无 |
| $4$ | $20$ | × | √ | × | 无 |
| $5$ | $20$ | × | × | × | 无 |
