题目描述
小 Z 在一块棋盘上玩游戏。这块棋盘是一个由 $n$ 个顶点和 $m$ 条边组成的无向连通图,图上的顶点编号为 $[1,n]$ 中的正整数。游戏开始时,每个顶点上都放有一个棋子,每个棋子上有一个 $[0,n−1]$ 中的整数,表示棋子的编号。不同棋子的编号互不相同。
每次操作时,小 Z 需要先选择棋盘上的一条边,这条边的一个端点此时放有 $0$ 号棋子。然后,小 Z 将这条边两个端点上的棋子交换。
现在你已经知道棋盘的模样,以及初始状态下每个顶点上的棋子编号。小 Z 想请你回答 $q$ 个询问。每个询问指定了棋盘的目标状态,你需要回答能否通过若干次操作,将棋盘由初始状态变为这个目标状态。
输入格式
第一行输入三个正整数 $n,m,q$,分别表示图中的顶点数、边数,以及询问的个数。
接下来 $m$ 行,每行两个整数 $u,v(1\leq u,v\leq n)$,表示图中有一条连接 $u,v$ 两顶点的无向边。保证 $u\neq v$ ,即图中不存在自环。保证给出的图是连通图,即任意两个顶点都可以经过若干条边而相互到达。
接下来一行有 $n$ 个空格隔开的整数,其中第 $i$ 个整数表示初始状态下 $i$ 号顶点上的棋子的编号,保证编号都为 $[0,n-1]$ 中的整数,且两两不同。
接下来 $q$ 行,每行有 $n$ 个空格隔开的整数,表示一个询问,其中第 $i$ 个整数表示目标状态中第 $i$ 号顶点上的棋子的编号,保证编号都为 $[0,n-1]$ 中的整数,且两两不同。
输出格式
输出 $q$ 行,每行一个字符串 Yes 或者 No(不含引号)作为回答。Yes 表示从棋子的初始状态可以经过若干次操作而达到询问中所指定的目标状态,No 表示不存在这样的操作步骤。注意:Yes 和 No 的首字母都是大写的。
样例
input
5 6 3
2 1
4 5
3 5
3 4
2 3
1 3
1 2 3 4 0
0 1 2 3 4
2 1 0 4 3
4 3 0 1 2output
Yes
Yes
No
样例 1 如下图所示:
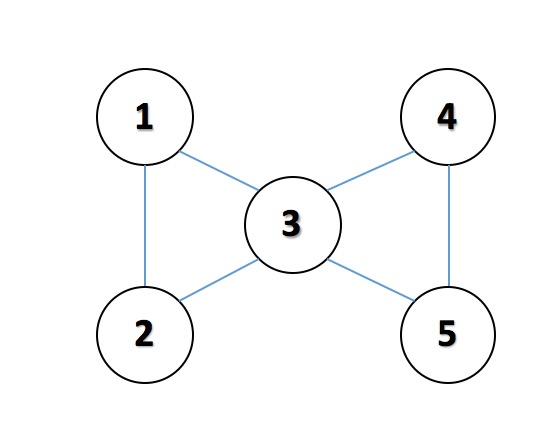
对于第一组询问,只要将 $0$ 号点沿着 $5−4−3−2−1$ 的路径移动。对于第二组询问,将 $0$ 号点沿着 $5−3−1−2−3$ 移动。对于第三组询问是无解的。
见附加文件。
数据范围与提示
| 测试点编号 | $n$ | $m$ | 数据特性 |
|---|---|---|---|
| 1 | $ \leq 8$ | $ \leq 15$ | 无 |
| 2 | $\leq 8$ | $ = n-1 $ | 无 |
| 3 | $\leq 50$ | $ = n-1 $ | 无 |
| 4 | $\leq 50$ | $ =n $ | 无 |
| 5 | $\leq 50$ | $ =n $ | 特性1 |
| 6 | $\leq 50$ | $ =n $ | 特性1 |
| 7 | $\leq 50$ | $ =n $ | 无 |
| 8 | $\leq 50$ | $ =n $ | 无 |
| 9 | $\leq 50$ | $ \leq 100$ | 特性2 |
| 10 | $\leq 50$ | $ \leq 100$ | 特性2 |
| 11 | $\leq 50$ | $ \leq 100$ | 特性2 |
| 12 | $\leq 50$ | $ \leq 100$ | 特性2 |
| 13 | $\leq 50$ | $ \leq 100$ | 特性2 |
| 14 | $\leq 50$ | $ \leq 100$ | 无 |
| 15 | $\leq 50$ | $ \leq 100$ | 无 |
| 16 | $\leq 50$ | $ \leq 100$ | 无 |
| 17 | $\leq 50$ | $ \leq 100$ | 无 |
| 18 | $\leq 50$ | $ \leq 100$ | 无 |
| 19 | $\leq 50$ | $ \leq 100$ | 无 |
| 20 | $\leq 50$ | $ \leq 100$ | 无 |
