题目描述

译自 POI 2011 Round 3. Day 1. B「Inspection」

Byteotia 铁路网包含了一些连接着火车站的双向铁路。每一对车站至多被一段铁路相连。此外，从任意一个火车站出发，到另一个火车站有且只有一条路径。（这条路径可能包括一些段铁路，但是不会重复经过任何火车站）。

Byteasar 是 Byteotia 铁路（BR）的一名卧底检查员。他的工作是挑选一个火车站（记这个火车站为 $S$）作为他操作的中心，然后前往所有其他的车站。他的检查旅程如下所示：

• Byteasar 从火车站 $S$ 出发；
• 接下来，他会挑选一个他还没去过的车站，然后沿最短路径前往该车站（当然是乘火车），然后视察这个车站，最后回到 $S$；
• BR 的不法员工会互相警告 Byteasar 的到来。为了瞒过他们，下一个车站 Byteasar 会到从 $S$ 出发并和上一次方向不同的车站视察，即，他会沿着与上次不同的铁路段离开 $S$；
• 每个火车站（除了 $S$）都恰好被视察一次；
• 在视察完最后一个车站后，Byteasar 不会回到 $S$。

通过一段铁路的时间都相同：一小时。

Byteasar 打算把每一个车站作为起始车站 $S$。对于每个火车站，Byteasar 想知道按某种顺序视察除 $S$ 以外的车站所用的最小时间，或者不可能把这个车站作为起始车站。

输入格式

第一行一个整数 $n$，表示车站数，车站从 $1$ 到 $n$ 编号；

接下来 $n-1$ 行，每行两个整数 $a,b$，表示 $a,b$ 车站之间有一段铁路。每个铁路段恰好出现一次。

输出格式

输出 $n$ 行，每行包含一个整数。对于第 $i$ 行，如果 $i$ 号车站可以作为初始车站，则输出对于 $S=i$，视察所有车站的最小用时，否则输出 $-1$。

样例

input

9
3 6
2 4
2 6
2 5
1 7
2 7
8 9
7 8

output

-1
23
-1
-1
-1
-1
-1
-1
-1

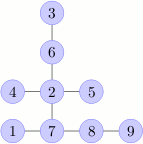
上图展示了在样例中给出的铁路网。只有当 $S=2$ 时才有可能视察到所有车站。一种最优的视察顺序是：$ 7, 4, 8, 6, 1, 5, 3, 9 $。最小用时 $23$ 小时。

数据范围与提示

对于全部数据，$ 1 \le n \le 1000000, 1 \le a, b \le n , a \neq b $；

对于 $30\%$ 的分数，$ n \le 2000 $。

Task authors: Wojciech Rytter and Bartosz Szreder.