题目描述

译自 POI 2011 Round 3. Day 1. A「Party」

Byteasar 打算举行一次聚会。他自然想要这次聚会成功进行。此外，Byteasar 确信只要邀请的嘉宾都互相认识就可以了。他目前在试着写一份邀请名单。

Byteasar 有 $n$ 个朋友，这里 $n$ 可以被 $3$ 整除。幸运的是，Byteasar 的朋友大部分都互相认识。并且 Byteasar 想起了一次他参加的聚会，那次聚会有 $ \frac{2}{3}n $ 个他的朋友参加，并且他们都互相认识。不幸的是，关于那次聚会的具体细节他不记得了……总的来说，他忘了是他的哪些朋友参加了。

Byteasar 认为他没有义务举办一个大型聚会，但他想邀请至少 $ \frac{n}{3} $ 个他的朋友。他不知道邀请谁，所以请你帮他。

输入格式

输入的第一行包含两个整数 $n,m$，表示 Byteasar 的朋友数和互相认识的朋友对数；

接下来 $m$ 行，每行两个整数 $a_i,b_i$， 表示朋友 $a_i,b_i$ 互相认识。每一对数最多在输入中出现一次。

输出格式

按编号升序，输出一行 $ \frac{n}{3} $ 个数，表示 Byteasar 要邀请的朋友编号。如果有多组解，输出任意一组均可。

样例

input

6 10
2 5
1 4
1 5
2 4
1 3
4 5
4 6
3 5
3 4
3 6

output

2 4

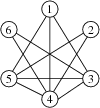
编号为 $1,3,4,5$ 的朋友互相认识。然而对于任意一对互相认识的朋友，如 $2,4$，都可以作为正确答案。即，这一对朋友并不一定来自于之前提到的那个四元组。

数据范围与提示

对于全部数据，$ 3 \le n \le 3000 , \frac{\frac{2}{3}n(\frac{2}{3}n-1)}{2} \le m \le \frac{n(n-1)}{2}, 1 \le a_i \lt b_i \le n $。

Task author: Jakub Onufry Wojtaszczyk.