题目描述
译自 POI 2011 Round 3. Day 0. A「Dynamite」
Byteotia 山洞由 $n$ 个洞穴和连接这些洞穴的 $n-1$ 条过道组成。对于每一对洞穴,从一个洞穴到达另一个都有唯一的路径,并且不需要离开山洞。炸药放在了某些山洞中。每条过道都放了引线。在每个洞穴中,相邻过道的引线交于一点,如果洞穴中有炸药,那么它们会与炸药相连。相邻两个洞穴之间的引线燃尽都恰好需要一单位时间。并且只要火传到了有炸药的洞穴中,炸药就会立即爆炸。
我们希望点燃 $m$ 个洞穴的引线(在引线的交点处点燃),使得引线引燃后,所有炸药在最短时间内爆炸。写一个程序求出这个最小可能时间。
输入格式
第一行包含两个整数 $n,m$,分别表示山洞中洞穴的个数和可以点火的引线数;
接下来一行 $n$ 个整数 $d_i$,如果 $d_i=1$ 则 $i$ 号山洞中有炸药,如果 $d_i=0$ 则没有。
接下来 $n-1$ 行,每行两个整数 $a,b$,表示一条过道连接洞穴 $a$ 和洞穴 $b$。
输出格式
一行一个整数,表示引爆所有炸药所需的最短时间。
样例
input
7 2
1 0 1 1 0 1 1
1 3
2 3
3 4
4 5
5 6
5 7output
1
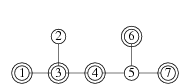
我们可以点燃洞穴 $3,5$ 中的引线。洞穴 $3$ 的炸药在时间 $0$ 时被引爆,洞穴 $1,4,6,7$ 内的炸药都在一单位之间后被引爆。
数据范围与提示
对于所有数据,$ 1 \le m \le n \le 3\times 10^5,d_i \in {0, 1},1 \le a \lt b \le n $;
对于 $10\%$ 的分数,$n\le 10$;
对于 $40\%$ 的分数,$n\le 10^3$。
Task author: Jacek Tomasiewicz.
