题目描述

译自 POI 2011 Round 2. Day 1. B「Garbage」

给定一张 $n$ 个点 $m$ 条边的无向图，每条边居黑白二色之一，且有一个黑或白的目标颜色。

有一辆卡车，可以从任意一个结点开始，经过一个简单环（不经过重复边或起点以外结点的环）回到出发点，将所有经过边的颜色反转，即黑色变为白色，白色变为黑色。卡车可以从不同的结点出发行走若干次。

请给出一个合法的方案，使得每条边最终都变为目标颜色，或判定不可行。

输入格式

输入的第一行包含两个空格分隔的正整数 $n$ 和 $m$（$1 \leq n \leq 100\,000$，$1 \leq m \leq 1\,000\,000$），表示图的点数和边数。

接下来 $m$ 行，每行包含四个空格分隔的正整数 $a, b, s, t$（$1 \leq a \lt b \leq n$，$s, t \in {0, 1}$），表示一条联结结点 $a$ 与 $b$ 的边，初始颜色和目标颜色分别为 $s$ 与 $t$。

你可以认为若存在合法方案，则存在一个卡车经过总边数不超过 $5m$ 的方案。

对于 $60\%$ 分数的数据，有 $m \leq 10\,000$。

输出格式

如果不存在合法方案，输出一行 NIE（波兰语「否」）；

否则按下列格式输出任意一种方案：

• 第一行包含一个整数 $k$，表示卡车行驶环路的总数；
• 接下来 $k$ 行，每行描述一条环路：
  • 首先是一个正整数 $k_i$ 表示环路经过的边数，后接一个空格；
  • 接下来 $k_i + 1$ 个空格分隔的整数，依次表示环路上结点的编号。

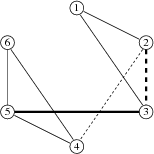
样例 1

input

6 8
1 2 0 1
2 3 1 0
1 3 0 1
2 4 0 0
3 5 1 1
4 5 0 1
5 6 0 1
4 6 0 1

output

2
3 1 3 2 1
3 4 6 5 4

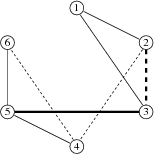
样例 2

input

6 8
1 2 0 1
2 3 1 0
1 3 0 1
2 4 0 0
3 5 1 1
4 5 0 1
5 6 0 1
4 6 0 0

output

NIE

数据范围与提示

Task author: Michal Pilipczuk.
SPJ: ceba.
Translation: Red Scarf.