题目描述
对于一个 $n$ 阶排列 $p$,我们建立一张无向简单图 $G(p)$,有 $n$ 个节点,标号从 $1$ 到 $n$,每个点向左右两侧最近的比它大的点以及比它小的点连边。
形式化地,在 $G(p)$ 中,$\forall u<v$,边 $(u,v)$ 存在当且仅当以下四个条件至少一个成立:
- $p_u<p_v$,且不存在 $u<i<v$ 满足 $p_u<p_i$;
- $p_u>p_v$,且不存在 $u<i<v$ 满足 $p_u>p_i$;
- $p_u<p_v$,且不存在 $u<i<v$ 满足 $p_i<p_v$;
- $p_u>p_v$,且不存在 $u<i<v$ 满足 $p_i>p_v$。
对于区间 $[l,r]$,规定其对应的排列 $p[l:r]$ 表示与 $pl,p{l+1},\cdots,p_r$ 大小顺序相同的 $(r-l+1)$ 阶排列。
例如,对于排列 $q={1,4,2,5,3}$,$q[2:4]$ 表示与 ${4,2,5}$ 大小顺序相同的 $3$ 阶排列,即 ${2,1,3}$。
无向图 $G$ 的最小染色数即给图的每个点染一种颜色,满足每条边的两端颜色不同,最少需要的颜色种类数。记为 $c(G)$。
现在给定一个 $n$ 阶排列 $p$,请你求出 $G(p)$ 的染色数,另外有 $q$ 次询问,每次询问一个区间 $[l,r]$,请你求出其所有子区间对应的排列的图的染色数最大值 $\mathrm{maxc}$,以及达到最大值的子区间个数 $\mathrm{cnt}$。
(形式化地,对于一对 $l,r$,求所有满足 $l\le l'\le r'\le r$ 的 $l',r'$ 中,$c(G(p[l':r']))$ 的最大值 $\mathrm{maxc}$,以及满足 $c(G(p[l':r']))=i$ 的 $l',r'$ 组数 $\mathrm{cnt}$。)
输入格式
第一行一个正整数 $n$。
第二行 $n$ 个正整数 $p_1,p_2,\cdots ,p_n$。
第三行一个整数 $q$。
接下来 $q$ 行每行两个正整数 $l,r$ 表示一组询问。
输出格式
输出共 $q+1$ 行,第一行一个正整数表示 $G(p)$ 的染色数,接下来每行两个整数 $\mathrm{maxc},\mathrm{cnt}$。
样例 1
input
6
1 4 5 3 6 2
5
1 6
1 3
2 5
2 6
3 3output
4
4 1
2 3
3 3
3 6
1 1
下图描述 $G(p)$ 及一种染色方案:
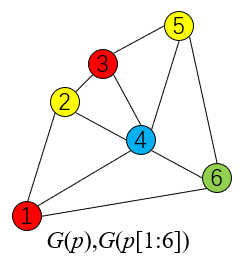
样例 2
input
6
1 4 5 3 6 2
5
1 6
1 3
2 5
2 6
3 3output
4
4 1
2 3
3 3
3 6
1 1
数据范围与提示
对于所有数据,$1\le n\le 3\times 10^5,0\le q\le 3\times 10^5$。
详细的数据限制及约定如下(留空表示和上述所有数据的约定相同):
| Subtask # | 分值(百分比) | $n$ | $q$ |
|---|---|---|---|
| $1$ | $10$ | $\le 10$ | $\le 10$ |
| $2$ | $15$ | $\le 100$ | $\le 10^4$ |
| $3$ | $15$ | $\le 2000$ | $\le 10^4$ |
| $4$ | $15$ | - | $=0$ |
| $5$ | $15$ | - | $\le 5$ |
| $6$ | $30$ | - | - |
