题目描述

小 L 和小 Q 在玩一个策略游戏。 有一个长度为 n 的数组 A 和一个长度为 m 的数组 B ，在此基础上定义一个大小 为 n × m 的矩阵 C ，满足 Cij = Ai × Bj。所有下标均从 1 开始。 游戏一共会进行 q 轮，在每一轮游戏中，会事先给出 4 个参数 l1, r1, l2, r2，满足 1 ≤ l1 ≤ r1 ≤ n, 1 ≤ l2 ≤ r2 ≤ m。 游戏中，小 L 先选择一个 l1 ∼ r1 之间的下标 x，然后小 Q 选择一个 l2 ∼ r2 之间 的下标 y。定义这一轮游戏中二人的得分是 Cxy。 小 L 的目标是使得这个得分尽可能大，小 Q 的目标是使得这个得分尽可能小。同 时两人都是足够聪明的玩家，每次都会采用最优的策略。 请问：按照二人的最优策略，每轮游戏的得分分别是多少？

输入格式

第一行输入 3 个正整数 n, m, q，分别表示数组 A，数组 B 的长度和游戏轮数。 第二行：n 个整数，表示 Ai，分别表示数组 A 的元素。 第三行：m 个整数，表示 Bi，分别表示数组 B 的元素。 接下来 q 行，每行 4 个正整数，表示这一次游戏的 l1, r1, l2, r2。

输出格式

输出共 q 行，每行一个整数，分别表示每一轮游戏中，小 L 和小 Q 在最优策略下 的得分。

样例数据

input

3 2 2
0 1 -2
-3 4
1 3 1 2
2 3 2 2

output

0
4

样例解释

这组数据中，矩阵 C 如下：

0 0

-3 4

6 -8

在第一轮游戏中，无论小 L 选取的是 x = 2 还是 x = 3 ，小 Q 都有办法选择某个
y 使得最终的得分为负数。因此小 L 选择 x = 1 是最优的，因为这样得分一定为 0。
而在第二轮游戏中，由于小 L 可以选 x = 2 ，小 Q 只能选 y = 2 ，如此得分为 4。

其他样例详见下方附件

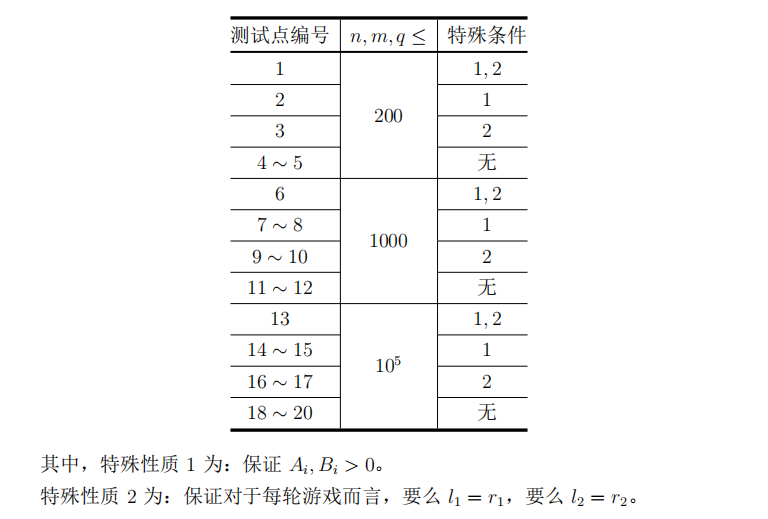
数据范围

对于所有数据，1 ≤ n, m, q ≤ 10^5, −10^9 ≤ Ai, Bi ≤ 10^9。对于每轮游戏而言，1 ≤l1 ≤ r1 ≤ n, 1 ≤ l2 ≤ r2 ≤ m。

附件下载

game.zip