祝大家AKCSP-J/S！AK xxywl！

卡这点发。。。

动态规划是多阶段决策，然后时间其实就是天然的状态，我们可以设$dp_i$为最后一次喝的时间是$i$的最多可以获得的美味值和。

我们现在知道了，所有倒酒的时刻都是偶数时刻，那么我们可以把他们压缩一下，然后存到一个时间线里面，比如说，一个数组$vc$它的每一个下标对应的都是一个向量。然后我们压缩之后，我们就设定：时刻$i$是先喝再倒，然后存到$dp$数组里面，所以我们每一次进来$i$都要更新一下$i-1$时刻倒的所有饮料的美味值。

接着，我们可以有一个$O(n^3)$的做法，对于每一个$dp_i$我们都暴力得回头望月，对于每一个望到底，在直接推过来。然后就得到了一个$O(n^3)$的，然后我们想想怎么优化。

首先，枚举每一个$i$是跑不掉的，接着，我们就要尽快找最优的$j$，为了方便理解，我举一个例子。

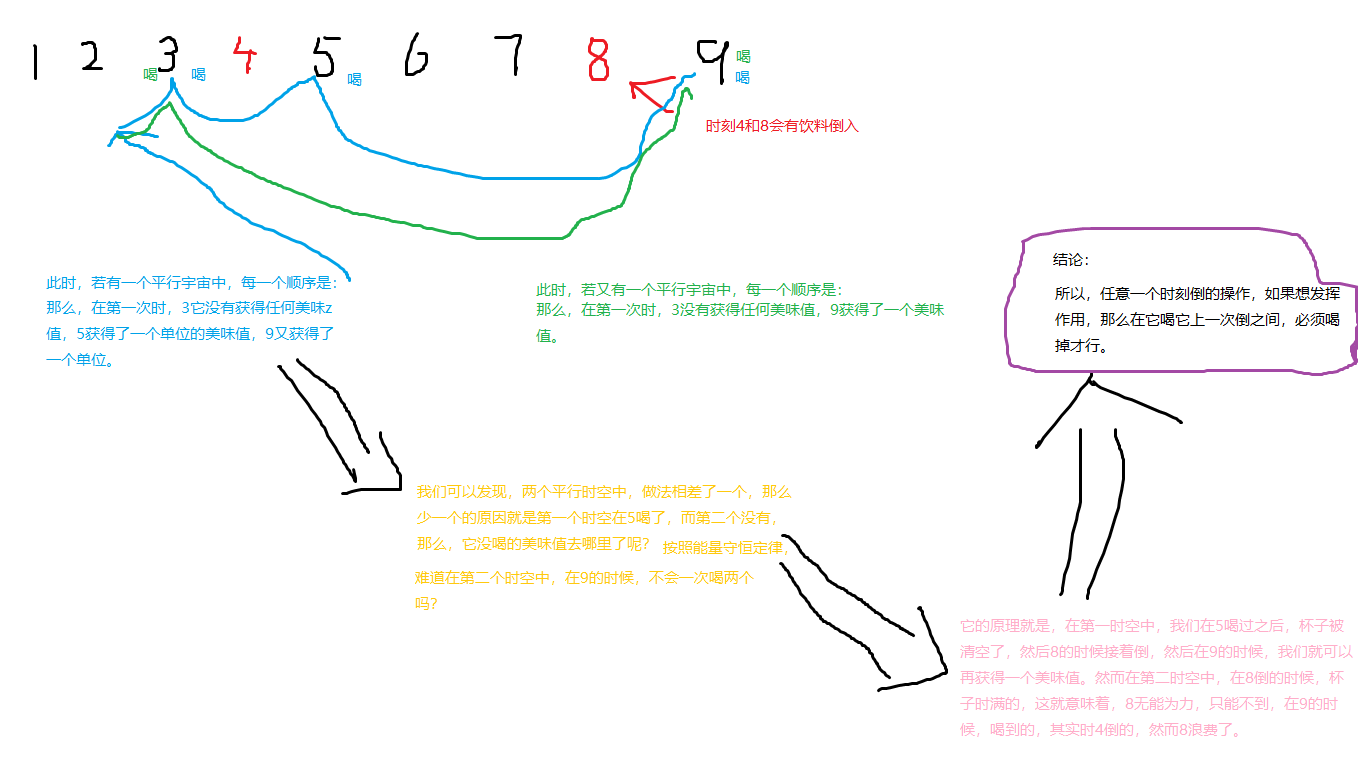
接下来，我们假设都不喝，然后我们根据上图推出的结果，我们可以推出一个不是转移方程的伪转移方程$dp_i=max(dp_1+val(1),dp_2+val(2)...dp[i-1]+val(i-1))$

其中，$val(x)$为：对于任意一种饮料，如果x向前若干个时刻，再向后若干个时刻，都有一个时刻中倒了这种饮料，那么，val(x)就要加上这种饮料的美味程度，然后把所有满足如上条件的饮料的美味值加一起，就是val(x)

接着，我们可以优化它，因为，没有人会在意一个算过的$dp$值原来在转移前时怎样的，那么，我们可以每当我们意识到$x$时刻满足上面的条件，就把它加上这种饮料的美味值，然后我们要区间处理（上一次到这一次），时间复杂度$O(n^2)$

然后，区间处理，我们可以直接用延迟更新（懒标记）就行。

最后，对于每一个$dp_i$，直接选择之前每一个$dp$值中最大的（用上面方法更新过的）一个，直接复制就行了。

注：对于每一次获得一个$dp_i$，要打擂，毕竟之后它会变得连自己人都不认识^_^

ACCode:

#include<bits/stdc++.h>
#define int long long
using namespace std;
vector<int>vc[500005];
int w[500005];
int n;
int mx[2000005];
int dp[500005];
int tag[2000005];
int ans=0;
int lst[500005];
void push_down(int x){
    mx[x<<1]+=tag[x];
    tag[x<<1]+=tag[x];
    mx[x<<1|1]+=tag[x];
    tag[x<<1|1]+=tag[x];
    tag[x]=0;
}
void push_up(int x){
    mx[x]=max(mx[x<<1],mx[x<<1|1]);
}
void update(int p,int l,int r,int ql,int qr,int c){
    if(l>qr or r<ql) return;
    if(l>=ql and r<=qr){
        mx[p]+=c;
        if(l!=r){
            tag[p]+=c;            
        }
        return;
    }
    int mid=(l+r)>>1;
    if(tag[p]){
        push_down(p);
    }
    if(ql<=mid){
        update(p<<1,l,mid,ql,qr,c);
    }
    if(qr>mid){
        update(p<<1|1,mid+1,r,ql,qr,c);
    }
    push_up(p);
}
int query(int p,int l,int r,int ql,int qr){
    if(l>qr or r<ql) return 0;
    if(l>=ql and r<=qr){
        return mx[p];
    } 
    if(tag[p]){
        push_down(p);    
    }
    int mid=(l+r)>>1;
    int t1=-1e18;
    if(ql<=mid){
        t1=max(t1,query(p<<1,l,mid,ql,qr));
    }
    if(qr>mid){
        t1=max(t1,query(p<<1|1,mid+1,r,ql,qr));
    }
    return t1;
}
signed main(){
    cin>>n;
    for(int i = 1;i <= n;i++){
        cin>>w[i];
    } 
    for(int i = 1;i <= n;i++){
        int len;
        cin>>len;
        int x;
        for(int j = 1;j <= len;j++){
            cin>>x;
            vc[x/2].push_back(i); 
        }
    }
    memset(dp,-0x3f,sizeof (dp));
    dp[1]=0;
    for(int i = 2;i <= 500000;i++){
        for(auto x : vc[i-1]){
            update(1,1,500000,lst[x]+1,i-1,w[x]);
            lst[x]=i-1;
        }
        dp[i]=query(1,1,500000,1,i-1);
        update(1,1,500000,i,i,dp[i]);
        ans=max(ans,dp[i]);
    }
    cout<<ans<<endl;
    return 0;    
}

致谢：$njw cqy$（“试毒”）

刚开始学OI，买的东西：

电脑

鼠标

键盘

学OI半年，买的东西：

《算法导论》

《算法笔记》

《一本通》

学OI一年，买的东西：

《道德经》

《大悲咒》

木鱼

最近有点颓废，所以，如果我A不掉猪国杀，我就把JCX微信删了！！！

所有人，除了我和卢瀚佑都过了初赛，我真就是一个傻逼。

王昊宸，【数据删除】又【数据删除】 他的【数据删除】和【数据删除】 他就是一个【数据删除】

第4周工作日刷题记录

CodeForces

• 1878A

  greedy

• 1879A

  greedy *800

• 1879B

  constructive algorithms greedy *900

Luogu

nothing

Atcoder

nothing

POJ

nothing

我的个人主页：leetcode.cn/u/tong-gui-c/

总算是100A了

膜拜对象：

同届大佬：王昊宸 眭鑫 叶号添 陈斯 吴迪

往届大佬：胥硕鑫 崔真言 马昊博 杨智博

在此祝大家，CSP-JS过初赛！！！

到时是哪位吃撑了的老师把我的博客给删了！！！

太缺德辣！！！

究竟是谁！？

@zuotingting

@乙鸟

首先说一下，一下算法仅限娱乐，请勿在比赛中使用！！！

算法：猴子算法

空间复杂的：O（1）

时间复杂度（最坏情况）：O（n∞）

时间复杂度（最好情况）：O（n）

首先我们介绍无限猴子定理

无限猴子定理最早是由埃米尔·博雷尔在1909年出版的一本谈概率的书籍中提到的，此书中介绍了“打字的猴子”的概念。无限猴子定理是概率论中的柯尔莫哥洛夫的零一律的其中一个命题的例子。大概意思是，如果让一只猴子在打字机上随机地进行按键，如果一直不停的这样按下去，只要时间达到无穷时，这只猴子就几乎必然可以打出任何给定的文字，甚至是莎士比亚的全套著作也可以打出来。

根据猴子定理，如果我们不断用随机的数字组成一个数列，那么在无限长的时间里，这个数列在某次肯定会变成有序。

关于猴子定理的实现，网上也有很多实例，但是大部分都是和上述一样，生成随机数字的数列，然后验证是否有序，我觉得这样实际上并不一种排序，我理解的排序就是对现有的数列进行排序，因此实现时做了一定的改造

给出一个固定的乱序数列 随机从这个乱序数列中取出数字放在第一位，然后重复取数字放在第二位，第三位.... 验证新的数列是否有序 这样做能更好的切合排序的概念

接下来上代码：

import random

def check(arr):
    for i in range(1,n):
        if arr[i]<=arr[i-1]:
            return True
    return False

if __name__=="__main__":
    arr=list(map(int,input().split()))
    n=len(arr)
    while check(arr):
        for i in range(n):
            pos=random.randint(i,n-1)
            t=arr[i]
            arr[i]=arr[pos]
            arr[pos]=t
    print(arr)