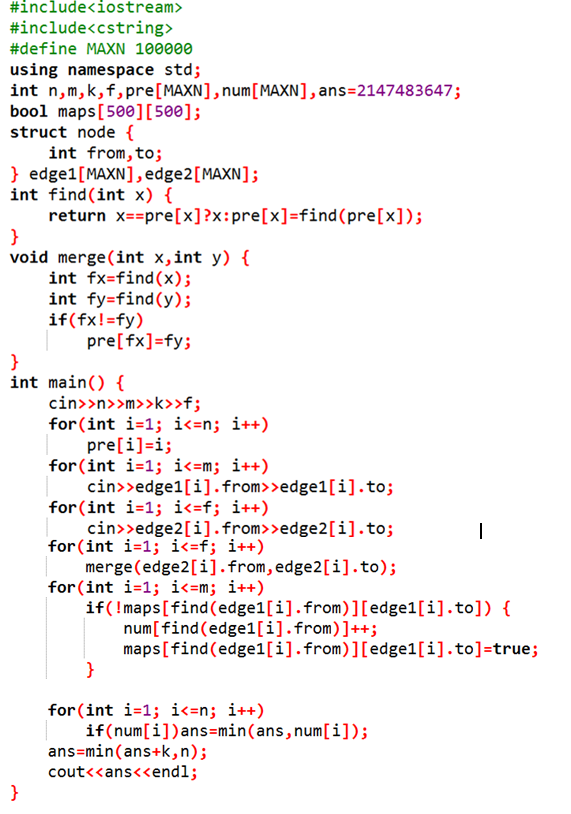
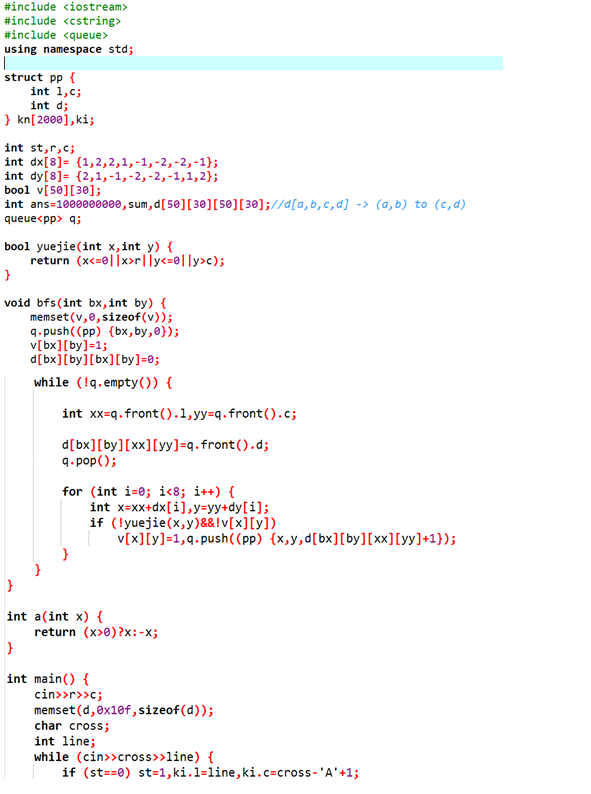
A.幸运数字

这道题的目的就是让我们判断数字是否为幸运数字。如何判断呢？既然要看每一位的数字，那么我们就要对数字进行拆分，拆分数字的程序大家应该是都很熟悉了，拆分完就可以找到数字的奇数位和偶数位了，即间隔数字相加求和，最后再判断这两个和是否相等就可以了。这里有同学可能会担心数据范围问题，a,b最大值到1000000，那么也就是对于一个数字来说最多进行7次循环就可以拆分完成，7×1000000不会超时。代码如下：

 #include <bits/stdc++.h>
using namespace std;
int s[7];
int a,b,ss;
bool check(int s[],int j){
    int ji=0,ou=0;
    for(int i=1;i<j;i++){
        if(i%2==1)
            ji+=s[i];
        else
            ou+=s[i];
    }
    if(ji==ou) return true;
    else return false;
} 
int main()
{
   cin>>a>>b;
   for(int i=a;i<=b;i++){
           memset(s,0,sizeof(0));
           int x=i;
           int j=1;
           while(x>0){
               s[j++]=x%10;
               x/=10;
           }
        if(check(s,j)){
            ss++;
        }
   }
   cout<<ss;
   return 0;
}

B.精密计时

这一类题目见到了之后，脑子里面就要闪现四个大字【统一单位】。对于这道题来说，格式很标准，每个字符串的第3个、第6个、第9个都是分隔符号，所以我们在处理的时候可以绕过它们，只对数字进行处理，字符转成其对应的数字处理这一步大家也非常熟悉了吧（不熟悉的同学要再多加练习！！！）处理过后全部转成百分秒的形式进行相减就ok了。（说个题外话，就算题目再让你以原格式输出，统一单位后也可以用取余再做处理，这不比借位要好理解多了）

#include <bits/stdc++.h>
using namespace std;
string s1,s2; 
int a[12],b[12],t1,t2;
int main()
{
   cin>>s1>>s2;
   for(int i=0;i<s1.size();i+=3){
           if(s1[i]=='0'){
               a[i]=s1[i+1]-'0';
           }
        else{
            a[i]=(s1[i]-'0')*10+s1[i+1]-'0';
        }
   }
   for(int i=0;i<s2.size();i+=3){
           if(s2[i]=='0'){
               b[i]=s2[i+1]-'0';
           }
        else{
            b[i]=(s2[i]-'0')*10+s2[i+1]-'0';
        }
   }
   t1+=a[9]+a[6]*100+a[3]*100*60+a[0]*100*60*60;
   t2+=b[9]+b[6]*100+b[3]*100*60+b[0]*100*60*60;
   cout<<t2-t1;
   return 0;
}

好了，你此时会想，这道题目也不算太长，那么就来看一种更短的操作，大声的告诉我scanf是什么！！！【格式化输入】——scanf(格式控制，&地址列表）;我们可以选用字符串中的：（冒号）和.(点）作为分隔符进行格式化输入，这样再按格式输入，就会自动跳过这些符号（这些在语法阶段的最后一课都有讲过噢，如果有同学看到这有点迷惑了，就要及时复习咯），所以我们的程序还可以这样：

#include<bits/stdc++.h>
using namespace std;
int main() {
    int h1,h2,m1,m2,s1,s2,b1,b2,t1,t2;
    scanf("%d:%d:%d.%d",&h1,&m1,&s1,&b1);
    scanf("%d:%d:%d.%d",&h2,&m2,&s2,&b2);
    t1=b1+s1*100+m1*100*60+h1*100*60*60;
    t2=b2+s2*100+m2*100*60+h2*100*60*60;
    cout<<t2-t1;
    return 0;
}

C.图像重组

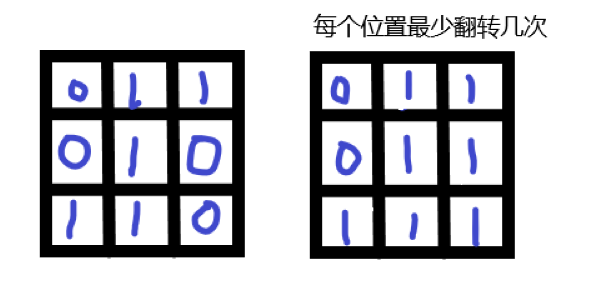
这道题看似复杂，实则不是很难（“老师说不难的题肯定很难”）。设想一下，现在这两张图在你的手上，你要怎么找重叠部分最大的位置。先两张图重叠起来，然后移动其中一张图，移一次看一次，移动的顺序就是上下左右来移动。那么这道题就是在模拟移动找重合的这个过程。假设重叠后上面的图是号1图，下面的图是2号图，2号图固定，1号图往左移，最多移n1，往右移，最多移n2，同理往上移最多移m1，往下移最多移m2。那我们就可以枚举上下左右移动的方式，每枚举一次，记录一次重叠部分的像素数量，然后进行打擂即可。

#include<bits/stdc++.h>   
using namespace std; 
int a[55][55],b[55][55];
int maxx;
int n1,m1,n2,m2; 
int main(){
    cin>>n1>>m1;
    for(int i=1;i<=n1;i++){
        for(int j=1;j<=m1;j++){
            cin>>a[i][j];
        }
    }
    cin>>n2>>m2;
    for(int i=1;i<=n2;i++){
        for(int j=1;j<=m2;j++){
            cin>>b[i][j];
        }
    }
    for(int dx=-n1;dx<=n2;dx++){
        for(int dy=-m1;dy<=m2;dy++){
            int cnt=0,ncnt=0;
            for(int i=1;i<=n1;i++){
                for(int j=1;j<=m1;j++){
                    int x=i+dx;
                    int y=j+dy;
                    if(x>=1&&x<=n2&&y>=1&&y<=m2){
                        if(a[i][j]==b[x][y]){
                            cnt++;
                        }
                        else{
                            ncnt++;
                        }
                    }
                }
            }
            if(ncnt==0){
                if(maxx<cnt){
                    maxx=cnt;
                }
            }
        }
    }
    cout<<maxx;
    return 0;
} 

D.程序分析

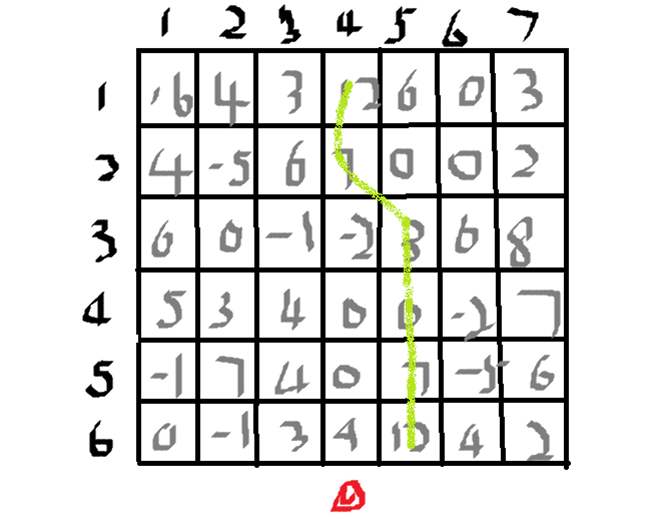
这题特别新颖，读程序我们都会，但是如何写程序去读程序。让我们把自己当做一台计算机。用计算机的思维去做。那就把X带进去执行一遍，就可以得到Y。这里提供的思路叫做边界值分析法。思路是我们可以解释执⾏程序，将⼀个具体的 x 值代⼊程序，就可以得到⼀个 y 的数值。 但解释执⾏有⼀个缺点：x 可以是所有 int 范围内的整数，因此枚举的代价很⼤。但同时，我们也观察到，对于许多 x 数值，程序的路径都是重复的，最终得到 y 的结果也是相同的，例 如： if (x > 9999) { if (x < 10000001) { y = 1; } } 对于上⾯的程序，对于任意的 10, 000 ≤ x ≤ 10, 000, 000，都会⾛⼊ y = 1 的路径——枚举这些x 是明显的浪费。 因此，我们只需要考虑 “导致条件变化” 的 x 数值——对于任意⽐较的常数 c，我们代⼊ c − 1, c, c + 1 即可触发所有与之相关的条件路径。在软件领域，这个技术被称为边界值分析。 我们需要做的事情有两件，一是把输入数据处理出来，变成分析额程序，同时找到所有的边界值。 二是把每个边界值带入程序，执行一遍。

#include<bits/stdc++.h>
using namespace std;
//语句结构体 
struct yuju{
    int op;  //命令1,2,3 
    char gx; // >，<，= 符号 
    int num; //数字 
}s[1010];
vector<int>tx; //用来存储x的临界点 
vector<int>ans;//用来存储y的取值 
int main(){
    int n;
    cin>>n;
    //接受语句，处理语句 
    for(int i=0;i<n;i++){
        char c;
        cin>>c;
        if(c=='}'){
            //命令3 }
            s[i].op=3;
        }else if(c=='y'){
            //命令2 y=
            s[i].op=2;
            cin>>c;
            cin>>s[i].num;
            cin>>c;
        }else{
            //命令1 if() 
            s[i].op=1;
            cin>>c;
            cin>>c;
            cin>>c;
            cin>>s[i].gx;
            cin>>s[i].num;
            tx.push_back(s[i].num-1);
            tx.push_back(s[i].num);
            tx.push_back(s[i].num+1);
            cin>>c;
            cin>>c;
        }
    }
    tx.push_back(-100);
    tx.push_back(1000000100);
    for(int i=0;i<(int)tx.size();i++){
        //x 保存当前边界值 cnt记录当前处于第几层if cango用于记录能否进入这一层if 
        int cnt=0,y=0,cango=0,x=tx[i];
        for(int j=0;j<n;j++){
            if(s[j].op==1){
                cnt++;
                if(s[j].gx=='>'){
                    if(x>s[j].num&&cango==cnt-1){
                        cango=cnt;
                    }
                }else{
                    if(x<s[j].num&&cango==cnt-1){
                        cango=cnt;
                    }
                }
            }
            if(s[j].op==2){
                if(cango==cnt){
                    y=s[j].num;
                }
            }
            if(s[j].op==3){
                if(cango==cnt){
                    cango--;
                }
                cnt--;
            }
        }
        ans.push_back(y);
    }
    sort(ans.begin(),ans.end());
    for(int i=0;i<(int)ans.size();i++){
        if(i==0){
            cout<<ans[i]<<" ";
        }else if(ans[i]!=ans[i-1]){
            cout<<ans[i]<<" ";
        }
    }
    return 0;
}

程序比较复杂，详细解释请观看解析视频。

A 最接近

这道题做对的同学还是很多的，但有一部分同学的错误原因是“不超过!!!!!”，转换成数学语言就是小于**等于**，要我们求出不超过N的最大的2的幂次方的正整数，可以先循环找出第一个超过N的2的幂次方的正整数，那它的上一个幂次方就是我们要找的答案了。数据范围在10^18，记得用long long.

B 序列

这道题的数据范围打败了所有人。题目给到X最大到10^30，大约在2^100（对对数有一定了解的同学可以解一下这个方程10^30=2^x,求出来x大约为100），而long long 最大可以保存2^63-1,所以long long已经不能作为本题的数据类型了。看到有同学（@@徐佳元）表示unsigned __int128可以使用，其实double就可以解决这个问题，double的数据最大可达1.79E+308。说完数据类型，来思考一下这题的解决思路，我们可以把a1~an视作一组进行累加求出和sum，看x中包含多少组，即x/sum组，那么到x/sum组结束后，k就为x/sum*n，接下来再在sum中依次累加a1~an，直到和大于x。注：用了double的地方，做除法的时候要注意取整，毕竟不管是下标还是组号都应该是整数。

C 互质

这道题题目中提到说数论是“数学的皇后”，于是所有使用穷举找互质的孩子们都被皇后打败了T-T。。因为如果使用穷举，那么程序最多执行N*M次，也就是10^11次，×超时。所以我们换一种方法。首先我们使用埃氏筛法将m以内的所有质数合数标记起来。因为一个数与另一个数互质有这么几种情况：①1与任何数都互质②如果两个数都是质数，那么他们绝对互质③如果其中有一个是合数，那么当质数与合数的质因数互质的情况下，他们也互质④如果两个数都是合数，那么他们两个不含有相同的质因数的情况下互质。接下来就开始判断1~m中的数字是否满足以上情况，如果满足，就是我们要找的答案了

D 矩阵

由于题目中提到每一步都是向下或者向右走，那么当前位置是否需要再次翻转就可以根据上一步的位置来决定。如果当前位置是0，不需要翻转，那么当前位置的翻转次数最小就是它的上一个或左一个的最少翻转次数。如果当前位置是1，那么需要根据它上一格或左一格是否为1来决定，如果是1，那么可以和前一次一起翻转，翻转次数不变；如果为0，那就要在最少翻转基础上再增加一次翻转。（以上文字请结合下图阅读）。

A.搭积木

首先根据数据范围来看，这道题目使用搜索肯定是行不通的。那么首先排序是一定的，假设最下面为第一层，最上面为第n层，那么从第一层到第n层每层都有a[i]种搭法，再利用乘法原理解决。但每层积木并不是可以随便摆，比如按样例中，第1层摆1，那么100就没办法摆上，所以第i层摆的积木一定要能承担还未摆放的积木中最大的一块。

B.跳格子

这道题我们可以反向处理，反着跳格子我们就可以得出当前位置的权值是由下方、左下方或者右下方走来的。再加上问题想要获得最高分，那么我们可以选择这三个位置中的最大值再加上当前位置的权值，所以可得f[i][j]=max(max(f[i-1][j],f[i-1][j-1]),f[i-1][j+1])+a[i][j];而且题目提到，游戏开始时玩家是在最后一行的中点下面，而不是在最后一行的中点，那么在最后一行，玩家起点位置的上方、左上方、右上方都有可能被选择到，所以最后的输出结果是这三个位置的最大权值。

C. 破冰游戏

在不考虑强制玩游戏的前提下，我们可以根据样例得出这样一个关系图。女员工之间会形成几个连通块，同一个连通块中的女员工都能选择与该连通块连接的男员工一起玩游戏，比如1号女员工可以与1号男员工玩，也可以和4号男员工玩，也可以和2号男员工玩，1号女员工可以玩三轮，2号女员工可以和3号男员工玩也可以和2号男员工玩，2号女员工可以玩2轮，所以本场最多玩两轮游戏，取最小值minn。另外每个女员工还能强制k个男员工与她玩游戏，所以游戏还可以能多进行k次，即minn+k。而且显然最多只能进行n场游戏，所以找出minn+k与n之间的最小值就是答案。

D.小狼棋

先不考虑狼王，我们可以先依次枚举汇合点，用宽搜预处理出小狼在棋盘上每个能跳的点还需要多少步才能到达汇合点，但这一步处理并不是只处理最短路径，标记棋盘上所有小狼可以到达的点。 再枚举哪个小狼接（或都不接）狼王最优，得出总距离为其他小狼到汇合点的距离+“我”到国王附近的距离+国王到附近的距离+国王的附近到汇合点的距离。