题目描述

有一个 $n$ 行 $m$ 列共 $n \times m$ 个白色格子组成的矩形网格。

阿尔卡狄在网格上进行了若干（可能为零）次操作。第 $i$ 次操作中，阿尔卡狄选择了一个非空的行的集合 $R_i$ 和一个非空的列的集合 $C_i$。对于每个 $R_i$ 的元素 $r$ 和每个 $C_i$ 的元素 $c$，处在行 $r$ 和列 $c$ 交点处的格子被染成黑色。

有一条限制是，每一行和每一列均只能最多被选择一次。换言之，不存在有序整数对 $(i, j)$（$i \leq j$）满足 $R_i \cap R_j \neq \varnothing$ 或 $C_i \cap C_j \neq \varnothing$，其中 $\cap$ 表示集合取并，$\varnothing$ 表示空集。

对于一个给定的网格最终染色情况，请判断它是否可以由一系列合法的操作得到。

输入格式

输入的第一行包含两个空格分隔的正整数 $n$，$m$ —— 分别表示网格的行数和列数。

接下来 $n$ 行每行包含 $m$ 个字符，每一个是 .（表示白色）和 #（表示黑色）之一，描述一个网格的染色情况。

输出格式

如果给定的网格可以由一系列合法的操作得到，输出 Yes；否则输出 No。

样例 1

input

5 8
.#.#..#.
.....#..
.#.#..#.
#.#....#
.....#..

output

Yes

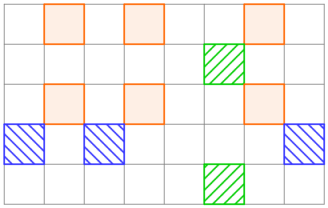
样例 1 给定的网格可以由三次操作得到，如下图。相同的颜色表示相同的操作。

样例 2

input

5 5
..#..
..#..
#####
..#..
..#..

output

No

样例 2 给定的网格无法由合法的操作得到。要将中间一行的格子染色，所有的列需要在一次操作中被全部选择；但这样一来，中间一列的另四个格子必然无法被染色。

样例 3

input

5 9
........#
#........
..##.#...
.......#.
....#.#.#

output

No

数据范围与提示

子任务 1　$1 \leq n, m \leq 50$；
子任务 2　$1 \leq n, m \leq 1000$。