题目描述
小朋友 你们好吗 还能记得 我是谁吗 我就是魔法元首まどか!
「和我签订契约,成为魔法元首吧!」
于是这天元首不明所以地被地外生物 Kyubey 忽悠去成为了魔法元首。不过在开始练习魔法之前,元首需要为自己的魔法选择一个代表色。
下图是一个明度最大(即,HSV 色彩空间中 $V = 100\%$)的单位圆色盘。色盘上任意一点的坐标为一个非负实数对 $(\alpha°, r\%)$($0 \leq \alpha < 360$,$0 \leq r \leq 100$),表示色相为 $\alpha°$、饱和度为 $r\%$ 的颜色。另一种理解是,$\alpha°$ 表示从联结圆心和纯红色点的射线顺时针到达该点所经过的角度,$\frac {r} {100}$ 是该点到单位圆圆心的距离。
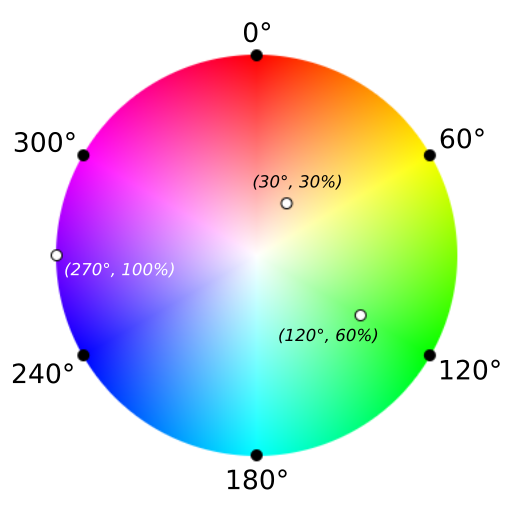
具体而言,从这个坐标 $(\alpha°, r\%)$ 到红绿蓝颜色值 $(R, G, B)$ 的转换如下:
$$ \begin{align} h &= \left\lfloor \frac{\alpha}{60} \right\rfloor \ f &= \frac{\alpha}{60} - h \ p &= 1 - (r\%) \ q &= 1 - f \times (r\%) \ t &= 1 - (1 - f) \times (r\%) \end{align} $$
$$ (R, G, B) = \begin{cases} (1, t, p), & \ \text{if} \ h = 0 \ (q, 1, p), & \ \text{if} \ h = 1 \ (p, 1, t), & \ \text{if} \ h = 2 \ (p, q, 1), & \ \text{if} \ h = 3 \ (t, p, 1), & \ \text{if} \ h = 4 \ (1, p, q), & \ \text{if} \ h = 5 \end{cases} $$
请参照样例确认你对公式的理解和实现。
按照 Kyubey 的判断,元首可以选择色盘所在的平面上一条给定直线段 $(\alpha_1°, r_1 \%)$–$(\alpha_2°, r_2 \%)$ 上的任意颜色。元首可不需要犹豫,作为一名 bling bling 的帝国领导者,当然要选择最亮的颜色啦!
一个颜色 $(R, G, B)$ 的亮度定义为 $L = 0.30R + 0.59G + 0.11B$。下图给出了彩色色盘和表示亮度的灰度色盘的左右对比。

你需要编写程序帮助元首计算给定直线段上所有颜色的最大亮度。
输入格式
从标准输入读入数据。
输入的第一行包含一个正整数 $T$ —— 数据的组数。接下来包含 $T$ 组数据,格式如下,数据间没有空行。
- 第 $1$ 行:四个空格分隔的整数 $\alpha_1$、$r_1$、$\alpha_2$、$r_2$。
输出格式
输出到标准输出。
对于每组数据输出一行,包含一个 $[0, 1]$ 范围内的十进制小数 —— 直线段 $(\alpha_1°, r_1 \%)$–$(\alpha_2°, r_2 \%)$ 上所有颜色的最大亮度,四舍五入保留恰好四位小数。数据保证若参考答案为 $A$,则 $[A - 10^{-5}, A + 10^{-5}]$ 范围内任意实数四舍五入到第四位小数后均相等。
样例
input
6
30 30 30 30
120 60 120 60
270 100 270 100
30 30 120 60
120 60 270 100
270 100 30 30
output
0.8785
0.7540
0.2600
0.9704
0.9408
0.8785
点 $(30°, 30\%)$ 的红绿蓝颜色值为 $(1.00, 0.85, 0.70)$,亮度为 $0.30 \times 1.00 + 0.59 \times 0.85 + 0.11 \times 0.70 = 0.8785$;
点 $(120°, 60\%)$ 的红绿蓝颜色值为 $(0.40, 1.00, 0.40)$,亮度为 $0.30 \times 0.40 + 0.59 \times 1.00 + 0.11 \times 0.40 = 0.7540$;
点 $(270°, 100\%)$ 的红绿蓝颜色值为 $(0.50, 0.00, 1.00)$,亮度为 $0.30 \times 0.50 + 0.59 \times 0.00 + 0.11 \times 1.00 = 0.2600$。
数据范围与提示
对于所有数据,有 $T \leq 100$,$0 \leq \alpha_1, \alpha_2 < 360$,$0 \leq r_1, r_2 \leq 100$。
| 测试点编号 | 附加限制 |
|---|---|
| 1 | $\alpha_1 = \alpha_2$,$r_1 = r_2$ |
| 2 | $\alpha_1 = \alpha_2$,$r_1 = r_2$ |
| 3 | $\alpha_1 = \alpha_2$ |
| 4 | $\alpha_1 = \alpha_2$ |
| 5 | $\alpha_1, \alpha_2 < 60$ |
| 6 | $\alpha_1, \alpha_2 < 60$ |
| 7 | $\lvert \alpha_1 - \alpha_2 \rvert < 60$,$r_1 = r_2$ |
| 8 | $\lvert \alpha_1 - \alpha_2 \rvert < 60$,$r_1 = r_2$ |
| 9 | 无 |
| 10 | 无 |
来自 [CodePlus](https://cp.thusaac.org/) 第 4 次月赛,清华大学计算机科学与技术系学生算法与竞赛协会 荣誉出品。 Credit:idea 与命题/吕时清 验题/朱玮昊 Git Repo:https://git.thusaac.org/publish/CodePlus4 感谢腾讯公司对此次比赛的支持。
