题目描述

日が暮れてる　年も暮れてる　途方に暮れちゃってる
黄昏降临，岁暮到来，路途变得一片迷茫

有一张 $n$ 个节点组成的无向图，点从 $1$ 至 $n$ 编号，图中没有重边和自环。我们不知道它的确切形态，但是它满足以下条件：

• 由任一节点至节点 $1$ 的最短路径（经过边数最少的路径）存在且唯一；
• 令 $\ell_i$ 表示由节点 $i$ 至节点 $1$ 的最短路径上边的数目，那么对于所有 $2 \leq i \leq n$，有 $\elli \geq \ell{i-1}$ 成立；
• 节点 $i$ 的度数给定，为 $d_i$，并且所有 $d_i$ 均等于 $2$ 或 $3$。

请计算满足条件的不同的图的数目，输出其除以 $10^9 + 7$ 的余数。两张无向图不同当且仅当存在点对 $(u, v) \ (1 \leq u < v \leq n)$ 使得其中一张图中 $(u, v)$ 间有边而另一张图中没有。

输入格式

输入的第一行包含一个正整数 $n$ —— 节点的数目。

第二行包含 $n$ 个空格分隔的整数 $d_1, d_2, \ldots, d_n$ —— 依次为节点 $1, 2, \ldots, n$ 的度数。输入保证所有 $d_i$ 之和为偶数。

输出格式

输出一个整数 —— 满足条件的不同的图的数目除以 $10^9 + 7$ 所得的余数。

样例 1

input

4
3 2 3 2

output

1

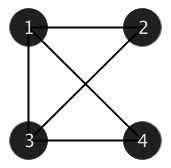
样例 1 中，满足条件的图有且仅有下图中的一张，其中节点 $2, 3, 4$ 至节点 $1$ 的最短路径均经过 $1$ 条边。

样例 2

input

5
2 3 3 2 2

output

2

样例 2 中，满足条件的图有且仅有下图中的两张。

样例 3

input

5
2 2 2 2 2

output

2

样例 4

input

20
2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 2 3 3 2

output

82944

数据范围与提示

$3 \leq n \leq 300$
$2 \leq d_i \leq 3$

子任务 1　$n \leq 10$；
子任务 2　$n \leq 50$；
子任务 3　$n \leq 80$；
子任务 4　没有附加限制。

遠回りでも　特別な道
即使迂回而行，亦是别样的旅途
遠回りでも　遠回りじゃない
即使迂回而行，也浑然不觉
　　　　　　　　　　　　——「帰り道」