题目描述

本题译自 eJOI2020 Problem B. Triangulation

注意：在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++
• C++ 11
• C++ 17
• C++ (NOI)
• C++ 11 (NOI)
• C++ 11 (Clang)
• C++ 17 (Clang)

Anna 画了一个正 $n$ 边形，多边形的 $n$ 个顶点分别用 $0$ 到 $n-1$ 的整数顺时针编号。之后她画了 $n-3$ 条对角线对其进行了三角剖分，这 $n-3$ 条对角线除多边形顶点以外没有任何交点。对角线指的是连接多边形两个不同且不相邻顶点的线段。

首先，定义顶点 $A$ 到对角线 $D$ 的距离。假设从顶点 $A$ 开始，沿顺时针方向不断移动至下一个顶点，直到到达对角线 $D$ 的某个端点，所经过的边数称为 left_distance。类似地，从 $A$ 开始沿逆时针方向移动，直到移动到对角线 $D$ 的某个端点，所经过的边数称为 right_distance。从 $A$ 到 $D$ 的距离是 left_distance 与 right_distance 的最大值。

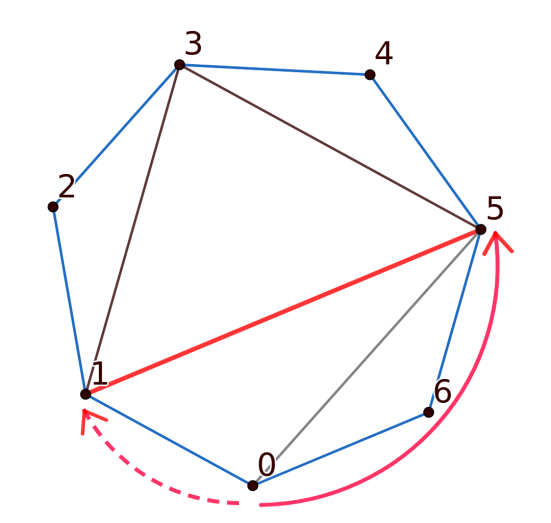
在这个样例图中，从顶点 $0$ 到对角线 $(1,5)$ 的距离是 $2$，left_distance 是 $1$，right_distance 是 $2$。从 $0$ 到对角线 $(0,5)$ 的距离是 $5$，left_distance 是 $5$，right_distance 是 $2$。

Anna 想给 Jacob 一个挑战性的任务。Jacob 不知道现在画了哪些对角线。他只知道 $n$ 的值，但是他可以多次询问 Anna 某些对顶点的信息，Anna 会告诉他在这些对顶点之间是否存在对角线。Jacob 的任务是找到距离顶点 $0$ 最近（距离的定义如上所述）的对角线。你需要帮助他在有限次数的询问后回答 Anna 的问题。

实现细节

你需要在提交中引入 triangulation.h 头文件，并实现如下函数：

• $\texttt{int solve(int n)}$
  • 这个函数会被 grader 恰好调用一次。
  • $n$：多边形的顶点数。
  • 如果答案为对角线 $(a,b)$ 离顶点 $0$ 最近，则函数应返回 $a\cdot n+b$。
  • 如果有多条对角线离顶点 $0$ 最近，你可以返回其中的任意一条。

上述函数可以调用以下函数：

• $\texttt{int query(int x, int y)}$
  • $x$：第一个顶点的编号。
  • $y$：第二个顶点的编号。
  • $0\le x,y\le n-1$
  • 如果 $x$ 与 $y$ 之间有一条对角线，则返回 $1$，否则返回 $0$。

数据范围与提示

对于全部数据，$5\le n\le 100$。

令 $q$ 为你在单组测试数据上询问的总数。令 $w=\frac{n\cdot (n-3)}{2}$。

• 如果你的询问不合法或你的答案错误，你会获得该测试点 $0\%$ 的分数；
• 如果 $w<q$，你会获得该测试点 $0\%$ 的分数；
• 如果 $n<q\le w$，你会获得该测试点 $10+60\cdot \frac{w-q}{w-n}\%$ 的分数；
• 如果 $q\le n$，你会获得该测试点 $100\%$ 的分数；

本题只有一组子任务，你的得分是每组测试数据得分之和。