题目描述
译自 ROI 2019 Day1 T3. Экспресс 20/19
给一个有 $n$ 个结点 $m$ 条边的 DAG。所有边均从编号小的结点指向编号大的结点。给出每条边的长度。
给一个常数 $p$。我们估计某条路径的总长度(这条路径上每条边的长度之和)为 $r$,而它的总长度实际上为 $x$,如果 $r⩽x⩽\frac{p}{p-1}\cdot r$,则称「估计这条(实长为 $x$ 的)路线的长度为 $r$ 是合理的」。
有 $q$ 组查询。第 $i$ 组查询包含两个数 $f_i,$ $r_i$。对于每组查询,试求是否存在一条以 $1$ 号结点为起点,以 $f_i$ 为终点的路径,满足:估计这条路线的长度为 $r_i$ 是合理的。
输入格式
每个输入文件包含多组数据。
文件的第一行:数据组数 $t$。
每组数据的第一行:$n$, $m$, $q$, $p$。
接下来 $m$ 行:$v_i$, $w_i$, $d_i$,表示一条边。
接下来 $q$ 行:$f_i$, $r_i$,表示一个查询。
输出格式
对于每组数据输出一行,每行一个长度为 $q$ 的 01 字符串 $s$。若 $s_i=1$,则在本组数据中第 $i$ 个查询是有解的;若 $s_i=0$,则在本组数据中第 $i$ 个查询是无解的。
样例 1
input
2
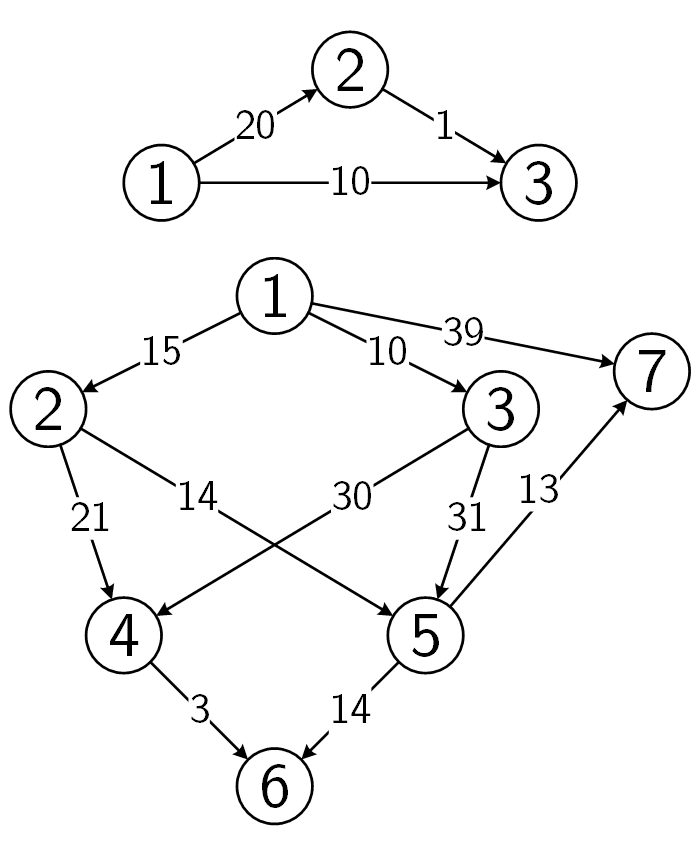
3 3 5 20
1 2 20
2 3 1
1 3 10
2 19
2 20
3 20
3 21
3 9
7 10 5 5
1 2 15
1 3 10
2 4 21
3 4 30
2 5 14
3 5 31
4 6 3
5 6 14
1 7 39
5 7 13
7 42
7 43
7 44
5 39
6 44output
11110
10111
样例 2
input
1
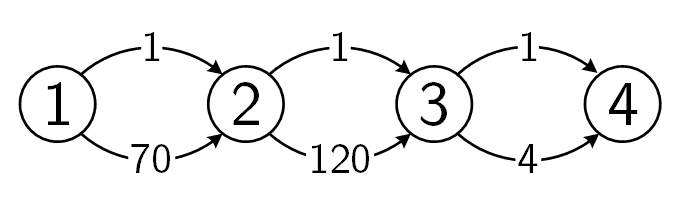
4 6 5 2
1 2 1
2 3 1
3 4 1
1 2 70
2 3 120
3 4 4
4 90
4 2
4 10
4 37
2 34output
11010
数据范围与提示
$1 ⩽ t ⩽ 1000,$ $2 ⩽ n ⩽ 500 000,$ $1 ⩽ m ⩽ 500 000,$ $1 ⩽ q ⩽ 500 000,$ $2 ⩽ p ⩽ 20,$ $, 1 ⩽ d_i ⩽ 10^{11},$ $1 ⩽ r_i ⩽ 10^{17}$. 保证 $\sum n,m,q⩽500000$.
| 子任务 # | 分值 | $n,m,q$ | 额外条件 |
|---|---|---|---|
| 1 | 15 | $n,m,q⩽10$ | |
| 2 | 24 | $\sum n,\sum m,\sum q⩽5000$ | $r_i⩽5000$ |
| 3 | 17 | $m=2n-2,q⩽10$ | $p=2$,DAG 是一条链 |
| 4 | 11 | $m=2n-2$ | DAG 是一条链 |
| 5 | 11$$ | $\sum n⩽1000,\sum m⩽2000$ | 所有 $r_i$ 相等 |
| 6 | 11 | 所有 $r_i$ 相等 | |
| 7 | 11$$ |
