题目描述
译自 ROI 2018 Regional. Day1 T4. Мониторинг труб
某输气系统包含 $n$ 个节点,编号分别为 $1\ldots n$,某些节点间有单向管道连接。1 号节点是中央储气设施。
节点系统可用数列 $p_2,$ $p_3,$ $\ldots,$ $p_n$ 来表示。对于 $i\in[\;!2,n\;!],$ $p_i$ 号节点会有一条通向 $i$ 号节点的单向管道。已知中央储气设施可以将气体输送到系统中的所有节点。输气系统包含不同种类的管道,用英文小写字母 a~z 来表示。$p_i$ 号节点通向 $i$ 号节点的管道的类型为 $c_i$。
有一种特殊的机器人被用来检查管道的质量。我们把「机器人从一个节点沿着一根管道前行到另一个节点,且机器人前进方向与气体方向一致」称作「一次移动」。
机器人会先被放在一个节点中,然后它会进行一次或多次移动,最后被人从输气系统中取出。这被称为「机器人进行了一次执勤」。
每次执勤时都需遵循 $m$ 种「规格」中的其中一种,这些规格的编号分别为 $1\ldots m$。每种规格都用一个由英文小写字母组成的字符串 $st_k$ 来表示。如果在一次执勤中机器人遵循了 $k$ 号规范,则在这次执勤中,机器人移动的次数与 $\mathrm{len}(st_k)$ 相等,并且对于 $i\in[1,\mathrm{len}(stk)],$ $st{k\:!,\;!j}$ 等于机器人第 $j$ 次经过的管道的编号。
若某次执勤遵循了 $t$ 号规格,则这次的花费为 $w_t$。
请问,要想让所有的管道都至少被检查一次,至少需要花费多少钱,并给出执勤路线的方案。
输入格式
$n,m,t$($t$ 的含义会在下面告诉你)
接下来 $n-1$ 行:$p_i,$ $c_i$
接下来 $m$ 行:$w_i,$ $st_i$
输出格式
第一行包含一个整数,表示最小花费。若无解请输出 -1.
若 $t=0$ 就不用管后续了,若 $t=1$ 且有解则需输出方案。
输出方案时,在第一行输出最小花费之后,第二行应包含方案中路径的数量 $k$,接下来 $k$ 行,每行包括三个整数 $a_i,$ $b_i,$ $c_i$,依次表示一条执勤路线的起点、终点,以及这次执勤所使用的规格。
样例 1
input
3 3 0
1 a
2 b
3 a
4 b
2 aoutput
6
样例 2
input
7 3 1
1 a
2 a
3 b
3 b
1 b
6 b
3 aab
5 b
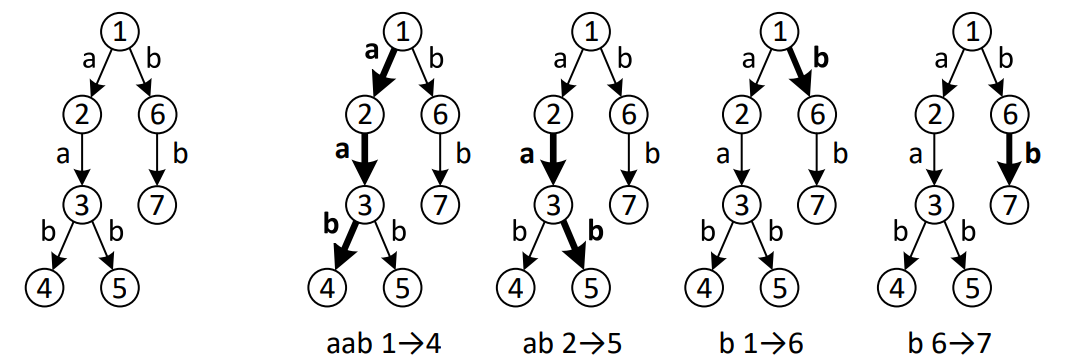
2 aboutput
15
4
1 4 1
2 5 3
1 6 2
6 7 2
数据范围与提示
对于所有数据,$1 ≤ n ≤ 500,$ $1 ≤ m ≤ 10^5,$ $t=0$ 或 $1,$ $1 ≤ p_i ≤ i-1,$ $1 ≤ w_i ≤ 10^9,$ $\sum \mathrm{len}(st_k) ≤ 10^6$.
| 子任务 # | 分值 | $n≤$ | $m≤$ | 特殊条件 | $t$ | 依赖的 子任务 |
|---|---|---|---|---|---|---|
| 1 | 9 | $500$ | $10^5$ | $\mathrm{len}(st_i)=1$ | $t = 0$ | |
| 2 | 10 | $500$ | $10^5$ | $p_i=i-1$ | $t = 0$ | |
| 3 | 22 | $15$ | $10^5$ | $t = 0$ | ||
| 4 | 20 | $500$ | $500$ | $t = 0$ | ||
| 5 | 19 | $500$ | $10^5$ | $t = 0$ | 1 – 4 | |
| 6 | 20 | $500$ | $10^5$ | $t = 1$ | 1 – 5 |
