题目描述

题目译自 JOISC 2014 Day4 T1「2 人の星座」

JOI 酱和 IOI 酱是一对亲密无间的好朋友。某天，JOI 酱与 IOI 酱决定去山上的某个观象台进行天体观测。
从观象台上可以观测到 $N$ 颗星星，编号为 $1\dots N$。每颗星星的颜色为红色、蓝色、黄色中的一种。
在观象台上观测到的星星可以用坐标系上的点来表示。在坐标系上，$i$ 号星对应的点为 $P_i$，位于 $(X_i,Y_i)$。坐标系上的点两两不同，且不存在三点共线。
JOI 酱和 IOI 酱想要设立一个叫做「JOIOI 座」的星座。首先。两个人决定使用红色、蓝色、黄色三种颜色的星各一个构成的三角形。他们将这样的三角形称作「好三角形」。 两人将满足以下条件的一对（两个，无序）好三角形作为「JOIOI 座的候补」：

• 两个三角形没有公共点（包括内部和边界）。换言之，两个三角形之间既不相交，也不存在某个三角形包含另一个三角形。

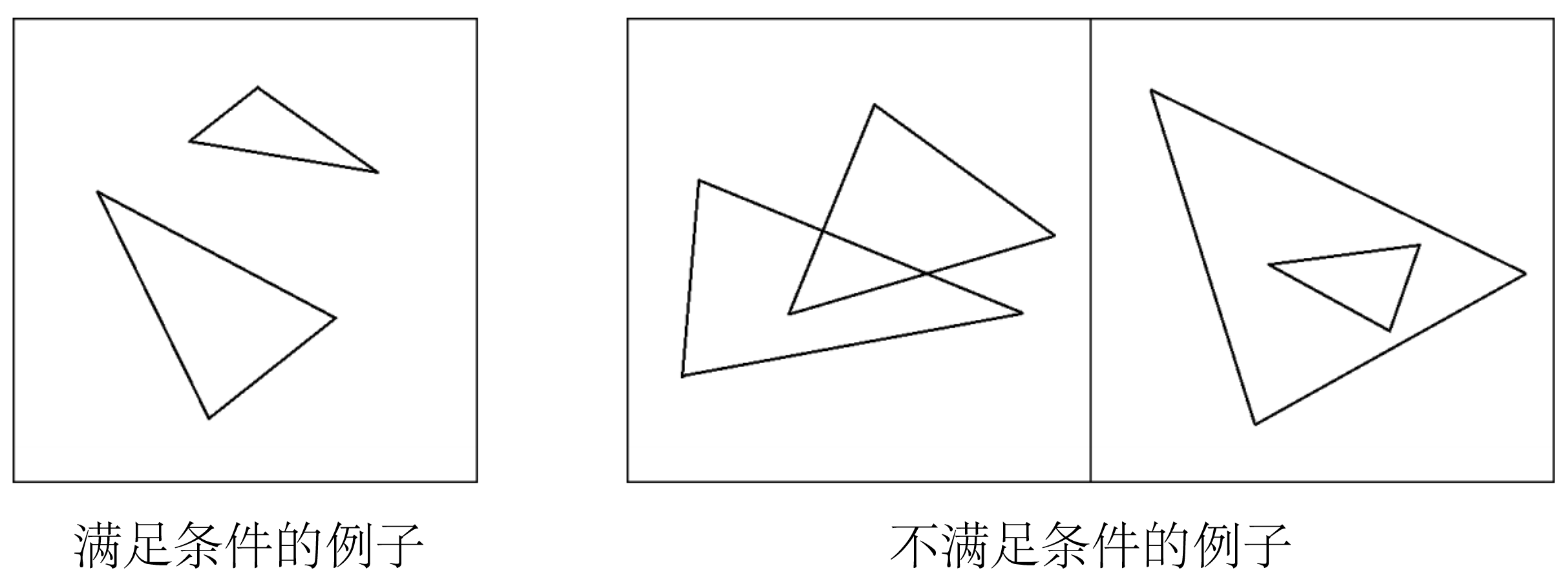
JOI 酱和 IOI 酱想知道构成 JOIOI 座的候补一共有多少种方案。
注意，如果构成三角形的 $6$ 个点一样，但是构成三角形的方式不同，算作不同的方案。
现在给出观象台上能观测到的星星的信息，请求出构成「JOIOI 座的候补」一共有多少种方案。

输入格式

第一行一个整数 $N$，代表展望台上能观测到的星星的数量。
接下来 $N$ 行，第 $i$ 行有三个空格分隔的整数 $X_i,$ $Y_i,$ $C_i$，表示 $i$ 号星的坐标为 $(X_i,Y_i)$，$C_i$ 表示 $i$ 号星的颜色，其中 $0$ 代表红色，$1$ 代表蓝色，$2$ 代表黄色。

输出格式

输出一行一个整数，表示 JOIOI 座候补的方案数。

样例 1

input

7
0 0 0
2 0 1
1 2 2
-2 1 0
-2 -3 0
0 -2 1
2 -2 2

output

4

星星的位置如下图。红星 -> 圆，蓝星 -> 菱形，黄星 -> 三角形。

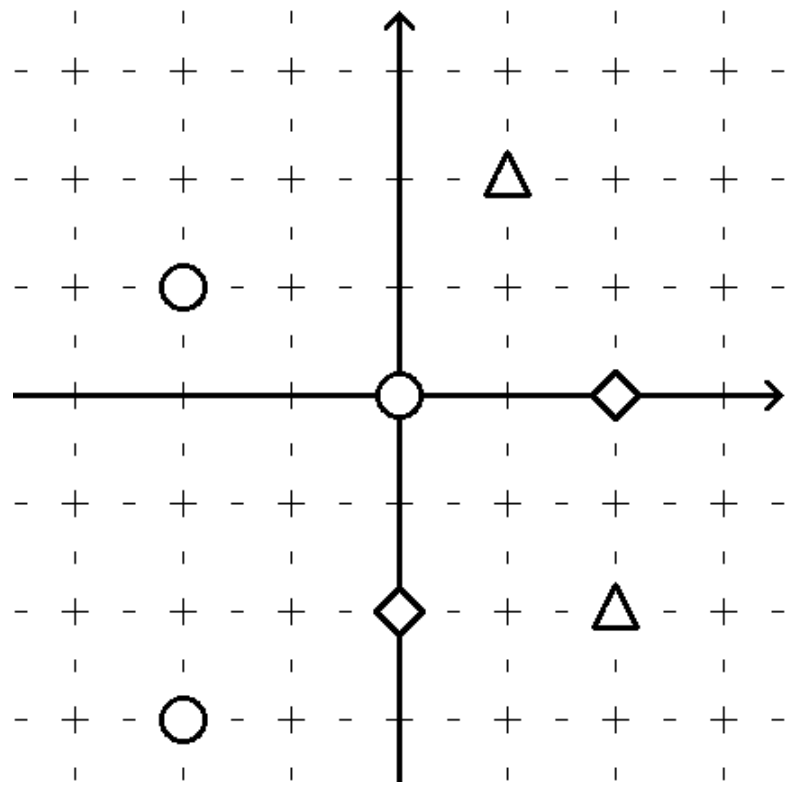
有四种 JOIOI 座的候补：

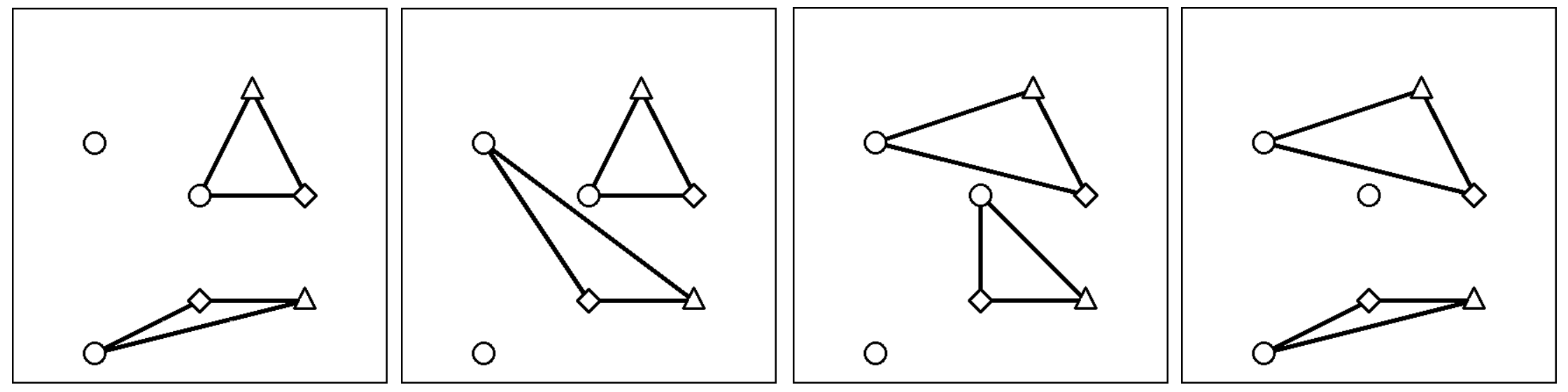
样例 2

input

8
16 0 0
17 0 0
0 7 2
0 -7 2
-1 -1 1
-1 1 2
-6 4 1
-6 -4 1

output

12

样例 3

input

21
1 20 0
4 20 0
0 22 0
5 22 0
6 25 0
8 25 0
4 26 0
11 11 1
7 12 1
14 13 1
8 15 1
15 16 1
11 17 1
18 0 2
13 2 2
16 2 2
19 4 2
18 6 2
21 8 2
24 8 2
19 10 2

output

7748

数据范围与提示

对于 $15\%$ 的数据，$N\le 30$。
对于另外 $40\%$ 的数据，$N\le 300$。
对于所有数据，$6\le N\le 3000,$ $-10^5\le X_i, Y_i\le 10^5,$ $C_i=0$ 或 $1$ 或 $2$，保证任何一种颜色的星星都有至少一颗，星星坐标互不相同，无三星共线。