题目描述
题目译自 JOISC 2014 Day3 T3「電圧」
你知道 Just Odd Inventions 公司吗?这个公司的业务是「只不过是奇妙的发明 / Just Odd Inventions」。这里简称为 JOI 公司。
JOI 公司的某个实验室中有着复杂的电路。电路由 $N$ 个节点和 $M$ 根细长的电阻组成。节点编号为 $1\sim N$。
每个节点可设定为两种电平之一:高电平或者低电平。每个电阻连接两个节点,只有一端是高电平,另一端是低电平的电阻才会有电流流过。两端都是高电平或者低电平的电阻不会有电流流过。
试求:有多少个电阻,可以通过调节各节点的电压,使得「没有电流流经该电阻,且其他 $M-1$ 根电阻中都有电流流过」。
对了,JOI 公司这个奇妙的电路是用在什么样的发明上的呢?这是公司内的最高机密,除了社长以外谁都不知道哦~
输入格式
第一行两个空格分隔的正整数 $N$ 和 $M$,表示电路中有 $N$ 个节点和 $M$ 根电阻。
接下来 $M$ 行,第 $i$ 行有两个空格分隔的正整数 $A_i$ 和 $B_i$ $(A_i≠B_i)$,表示第 $i$ 个电阻连接节点 $A_i$ 和节点 $B_i$。
输出格式
输出一行一个整数,代表电路维护时可选择的使其不流的电阻个数。
样例 1
input
4 5
1 2
1 3
1 4
2 4
3 4output
1
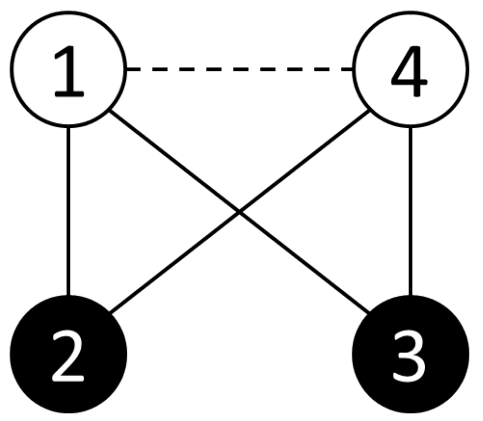
只能使第三根电阻中没有电流流过。做法:将结点 $1$ 和 $4$ 设置为高电平,结点 $2$ 和 $3$ 设置为低电平。
样例 2
input
4 4
1 2
2 3
3 2
4 3output
2
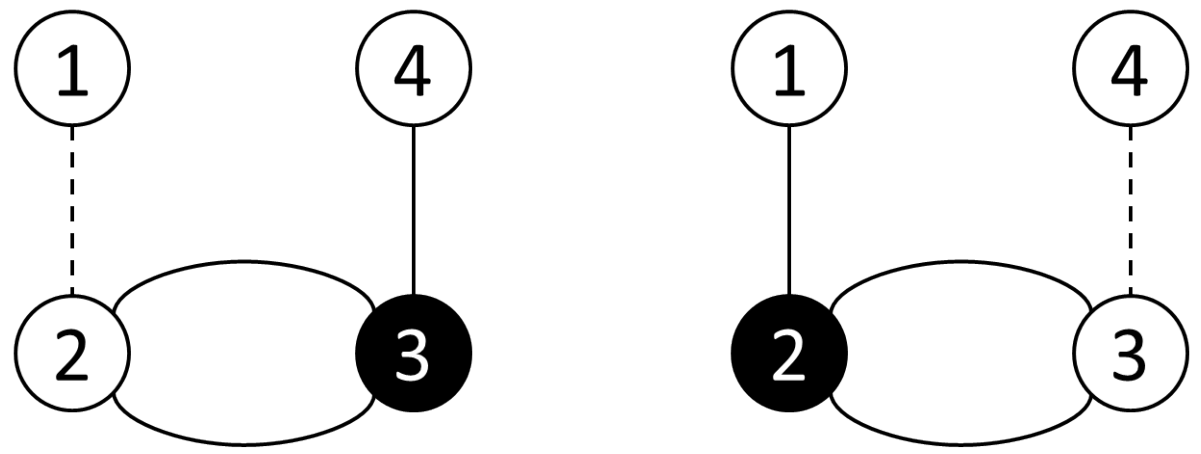
可以选择第一根电阻或第四根电阻。
样例 3
input
13 16
1 6
2 6
3 1
3 2
4 7
4 7
5 9
6 5
8 2
8 13
9 11
10 3
11 10
11 12
12 8
13 6output
3
数据范围与提示
对于所有测试数据,$2 \le N \le 10^5,$ $1 \le M \le 2\times 10^5$。不保证图是连通的,不保证没有重边。
| 子任务编号 | 分值 | $N, M$ | 保证图连通 |
|---|---|---|---|
| 1 | 10 | $N\le 1000,$ $M\le 2000$ | |
| 2 | 10 | $M=N$ | √ |
| 3 | 35 | $M\le N+100$ | √ |
| 4 | 45 |
