题目描述

题目译自 JOISC 2014 Day2 T3「スタンプラリー」

IOI 铁路是由 $N+2$ 个站点构成的直线线路。这条线路的车站从某一端的车站开始顺次标号为 $0\dots N+1$。

这条路线上行驶的电车分为上行电车和下行电车两种，上行电车沿编号增大方向行驶，下行电车沿编号减小方向行驶。乘坐这两种电车的话，移动 $1$ 站的距离需要 $T$ 秒。换句话说，乘坐上行电车从车站 $i$ 走到车站 $i+1$ 需要 $T$ 秒，乘坐下行电车从车站 $i$ 走到车站 $i-1$ 也需要 $T$ 秒。你不能在 $0$ 号车站乘坐下行电车，或在 $N+1$ 号车站乘坐上行电车。由于电车发车的频率非常高，你可以无视等待电车消耗的时间。

每个车站设有上行电车的站台和下行电车的站台，连接两个站台的道路上设有邮戳台。

现在，IOI 铁路召开了邮戳拉力赛。在拉力赛中，选手需要从0号车站的上行电车站台出发，在 $1\dots N$ 号车站各盖一枚邮戳，最终到达 $N+1$ 号车站的上行电车站台即可完成。

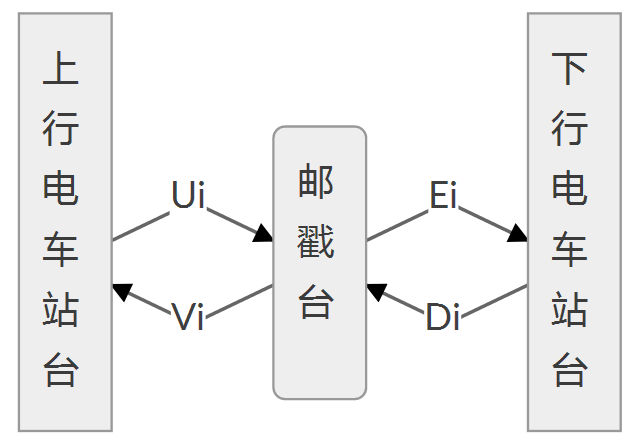
为了在每个车站盖上邮戳，必须从电车上下来，步行走到车站通路上的邮戳台。在 $i$ 号车站的上行电车站台、邮戳台、下行电车站台之间移动所消耗的时间如下所示：

• 从车站 $i$ 的上行电车站台到邮戳台的时间为 $U_i$ 秒；
• 从车站 $i$ 的邮戳台到上行电车站台的时间为 $V_i$ 秒；
• 从车站 $i$ 的下行电车站台到邮戳台的时间为 $D_i$ 秒；
• 从车站 $i$ 的邮戳台到下行电车站台的时间为 $E_i$ 秒；

邮戳拉力赛的选手在 $0$ 号车站与 $N+1$ 号车站都只能停留一次。$1\dots N$ 号车站都可以访问任意多次。

现在给出有邮戳台的车站个数、乘坐电车移动一站的时间、在每个车站的上行电车站台、邮戳台、下行电车站台之间移动所消耗的时间，请你求出完成邮戳拉力赛的最短时间。 这个时间包括从 $0$ 号车站出发，按下 $N$ 个邮戳后到达 $N+1$ 号车站的时间。无视等车的时间和按邮戳的时间。

输入格式

第一行两个空格分隔的整数 $N$ 和 $T$，表示有 $N+2个$ 车站，电车行驶一站的距离需要 $T$ 秒。
接下来 $N$ 行，第 $i$ 行有四个空格分隔的整数 $U_i,V_i,D_i,E_i$，分别表示：

• 从车站 $i$ 的上行电车站台到邮戳台的时间为 $U_i$ 秒；
• 从车站 $i$ 的邮戳台到上行电车站台的时间为 $V_i$ 秒；
• 从车站 $i$ 的下行电车站台到邮戳台的时间为 $D_i$ 秒；
• 从车站 $i$ 的邮戳台到下行电车站台的时间为 $E_i$ 秒。

输出格式

输出一行一个整数，表示完成邮戳拉力赛的最短时间。

样例 1

input

4 1
1 1 1 1
1 9 9 1
9 9 1 1
1 9 9 1

output

23

从车站 $0$ 出发，按照 $2\rightarrow 1\rightarrow 4\rightarrow 3\rightarrow 1\rightarrow 5$ 的顺序访问车站，可以达到最短时间。

样例 2

input

6 2
5 5 3 5
9 7 9 3
3 4 9 4
8 2 6 6
8 5 7 5
3 2 1 6

output

73

数据范围与提示

对于 $5\%$ 的数据，$N\le 16$。
对于另外 $75\%$ 的数据，$N\le 100$。
对于所有数据，$1\le N\le 3000,$ $1\le T\le 10^5,$ $1\le U_i,$ $V_i,$ $D_i,$ $E_i\le 10^5$。