题目描述
译自 BalticOI 2009 Day2 T2「Triangulation」
一个多边形的三角形划分是一个所有以该多边形的三个顶点组成的三角形的集合。这些三角形不能重叠且要覆盖整个多边形。
我们定义一次多边形切割以一条直线将一个多边形分为两部分。
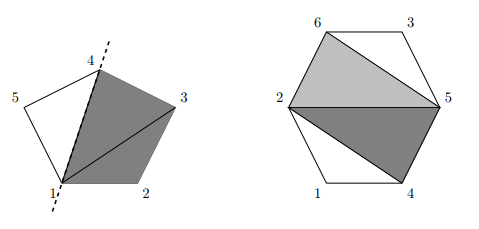
给定一个进行过三角形划分的凸多边形,每个三角形都有一个颜色。请找到保证没有两个相同颜色的三角形出现在不同的部分中的情况下最大的切割数量。
输入格式
第一行,一个整数 $n$,表示多边形的顶点个数。
顶点编号为 $1$ 到 $n$。
以下 $n-2$ 行,每行四个整数 $a,b,c$ 和 $d(1 \le a,b,c,d \le n)$,表示一个三角形的顶点为 $a,b,c$ 且它的颜色为 $d$。
$a,b,c$ 为三个不同的顶点。
保证三角形划分无误,且每个三角形都有色。
输出格式
一行,满足上述要求的最大的切割数量。
样例 1
input
5
1 2 3 2
4 5 1 1
3 1 4 2output
1
样例 2
input
6
1 4 2 1
2 4 5 2
6 2 5 3
3 6 5 1output
0
数据范围与提示
| 数据百分比 | 限制 |
|---|---|
| $50\%$ | $n \le 5000$ |
| $100\%$ | $3 \le n \le 100,000$ |
