题目描述

译自 JOISC 2018 Day1 T2「柵 / Fences」

JOI 君在 IOI 国拥有广阔的土地。

IOI 国的土地可以表示为一个平面直角坐标系。他的土地为坐标系上 $x,y$ 坐标满足 $x \in [-10^{100}\, , \, 10^{100}] \, , \, y \in [-10^{100}\, , \, 10^{100}]$ 的区域。他的牧场是在坐标系上 $x,y$ 满足 $x \in [-S\, , \, S] \, , \, y \in [-S\, , \, S]$ 的区域。

JOI 君要在牧场里修一些栅栏，来把牧场围起来，使得他的牛不可能从牧场内的任何一点走到他的土地之外。栅栏是一条长度为正实数的线段。牧场里已经有一些栅栏了。两个栅栏之间如果有共同点，那么它必然是至少一个的栅栏的端点。

JOI 君可以随意建栅栏。要求栅栏既不在牧场内，也不在 JOI 君的土地外，它们的长度任意，方向任意。他甚至可以修一条将整个牧场全围起来的栅栏。建造一条长度为 $l$ 的栅栏的费用是 $l$。两条栅栏可以相交，重合...... 怎么修都没问题（可参考样例）。

请你计算修栅栏的最小费用。

输入格式

第一行为整数 $N$ 和 $S$。

第 $i$ 行 $(1\le i \le N)$ 为四个整数 $A_i,B_i,C_i,D_i$ ，代表有一条连接点 $(A_i,B_i)$ 和点 $(C_i,D_i)$ 的栅栏。

输出格式

输出修栅栏的最小费用。

我们将会使用 SPJ。被允许的最大精度误差为 $0.01$。

样例 1

input

3 4
-3 5 1 8
-4 3 -4 6
5 1 7 2

output

29.0000000000

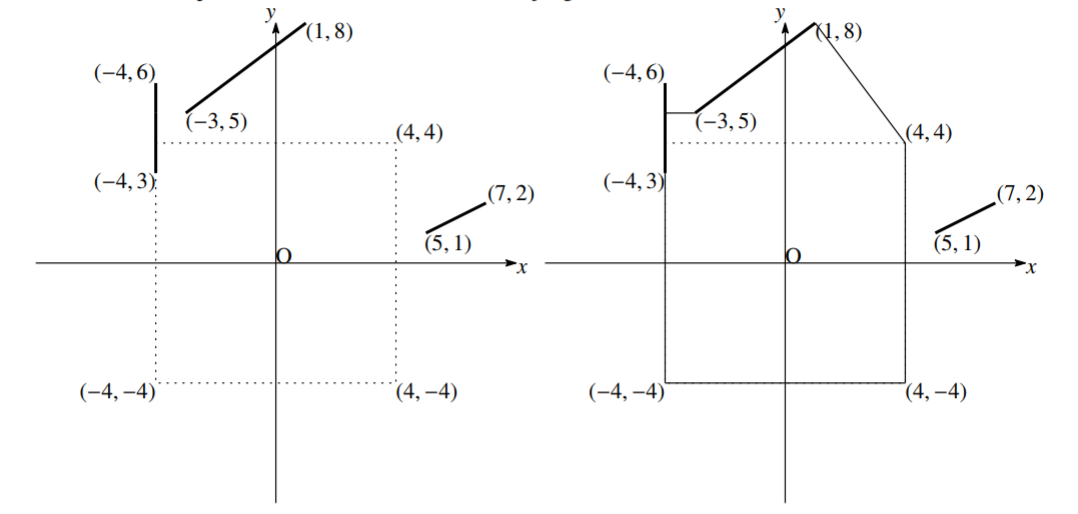
已经建好的栅栏见左图，点线为牧场的边界。

一种修栅栏的方法见右图。如果你输出 $29$ 或 $28.999$ 也对。

样例 2

input

1 2
-3 -3 -3 -2

output

16.0000000000

你根本用不到之前修好的任何栅栏。

样例 3

input

4 3
4 -1 3 4
-4 2 -2 4
-4 0 -5 6
0 -6 5 -2

output

14.1392801789

样例 4

input

10 80
175 95 60 -146
-106 57 18 185
190 -68 177 -142
84 -195 127 -179
34 143 126 69
-92 133 -190 80
-157 -66 -119 -161
-85 -124 129 -171
141 181 175 175
107 -38 150 148

output

238.4778364511

数据范围与提示

数据满足以下条件：

• $1 ≤ N ≤ 100 $．
• $1 ≤ S ≤ 200$．
• $ −200 ≤ A_i, B_i, C_i, D_i ≤ 200\, (1 ≤ i ≤ N)$．
• $(A_i, B_i) \ne (C_i, D_i)\, (1 ≤ i ≤ N)$．
• 没有栅栏经过牧场内部。
• 任意两个不同的栅栏，如果他们有公共点，那至少是一个栅栏的端点。

子任务 1（18 分）

$N=1$。

子任务 2（33 分）

$N\le 6$。

子任务 3（49 分）

没有额外限制。