「JOI 2014 Final」JOI 徽章 - Problem - HelloWorld信息学奥赛题库

日本信息学奥赛委员会为了应援将要去台湾参加 IOI 的选手们，打算制作一面新的 JOI 旗帜。JOI 旗帜为由 $ M $ 行 $ N $ 列的 $ M\times N $ 个正方形组成的图形，每个正方形里写有 J,O,I 中任一字母。

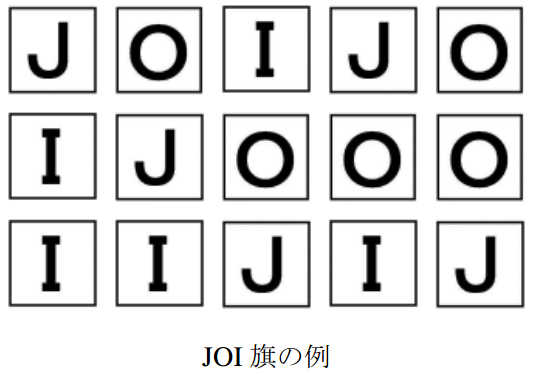
日本信息学奥赛委员会还决定制作 JOI 徽章 。JOI 徽章为由 $ 2 $ 行 $ 2 $ 列的 $ 4 $ 个正方形组成的图形，每个正方形里写有 J,O,I 中任一字母。

JOI 旗帜中所含 JOI 徽章的个数的意思是，与 JOI 徽章相同（不允许翻转或旋转）的 JOI 旗帜中的 $ 2\times 2 $ 区域的个数。

现在日本信息学奥赛委员会拥有一张旧的 JOI 旗帜和一张白纸。这张白纸的大小和一个构成 JOI 旗的正方形的大小相同。可以在这张白纸上写上 J,O,I 中任一字母。日本信息学奥赛委员会将进行以下任意一种操作来制作新的 JOI 旗帜。

日本信息学奥赛委员会想让新的 JOI 旗帜所含的 JOI 徽章的数量尽可能多。请求出新的 JOI 旗帜所含的 JOI 徽章的个数的最大值。

给出旧的 JOI 旗帜和 JOI 徽章的情况，请求出新的 JOI 旗帜所含的 JOI 徽章的个数的最大值。

输入标准如下：

第一行为两个以空格分开的整数 $ M,N $ 。表示旧的 JOI 旗帜是由 $ M $ 行 $ N $ 列的 $ M×N $ 个正方形组成的图形。
接下来的 $ M $ 行，每行为含有 $ N $ 个字符的字符串。每个字符为 J,O,I 中的一个。这 $ M $ 行中的第 $ i(1 \leq i \leq M) $ 行中从左数第 $ j(1 \leq j \leq N) $ 个字符表示旧的 JOI 旗帜上的第 $ i $ 行第 $ j $ 列的正方形中所写的字符。
接下来的 $ 2 $ 行，每行为含有 $ 2 $ 个字符的字符串。每个字符为 J,O,I 中的一个。这 $ 2 $ 行中的第 $ i(1 \leq i \leq 2) $ 行中从左数第 $ j(1 \leq j \leq 2) $ 个字符表示 JOI 徽章上的第 $ i $ 行第 $ j $ 列的正方形中所写的字符。

输出一行一个整数：表示新的 JOI 旗帜所含的 JOI 徽章的个数的最大值。

input

3 5
JOIJO
IJOOO
IIJIJ
JO
IJ

output

旧的 JOI 旗帜和 JOI 徽章和题目描述中的例子一样。从上面起第 $ 2 $ 行中，从左起第 $ 4 $ 列的正方形中的字符用白纸覆盖从而变为 'J' 。

像这样变化后的 JOI 旗帜含 $ 3 $ 个 JOI 徽章。

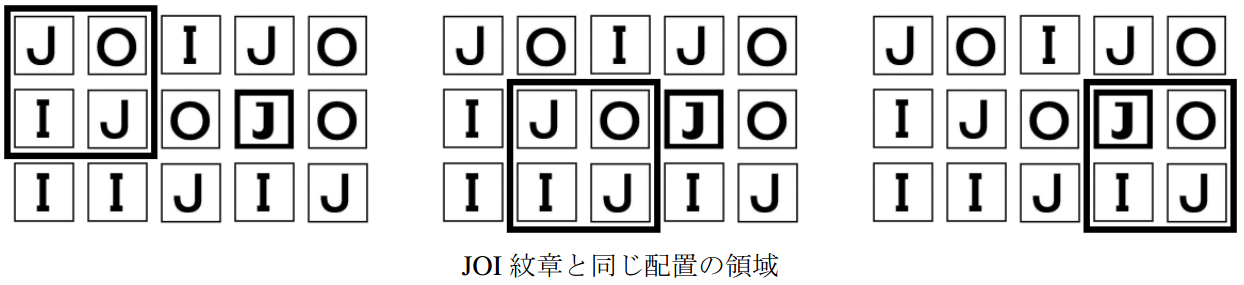
不存在能够包含 $ 4 $ 个 JOI 徽章的新的 JOI 旗帜。所以新的 JOI 旗帜所含的 JOI 徽章的个数的最大值为 $ 3 $ 。

input

2 6
JOJOJO
OJOJOJ
OJ
JO

output

请注意：存在不使用白纸而能达到最大值的情况。

input

2 2
JI
IJ
JJ
JJ

output

在输入样例 $3$ 的情况下，对于任何可能的新的 JOI 旗帜，都不可能含有 $ 1 $ 个 JOI 徽章。

对于 $ 30\% $ 的分值：

对于 $ 100\% $ 的数据，满足以下条件。

HelloWorld信息学奥赛题库