题目描述

有向图 $ G $ 有 $ n $ 个顶点 $ 1 , 2 ,\cdots, n $，点 $ i $ 的权值为 $ w(i) $。现在有一只蚂蚁，从给定的起点 $ v_0 $ 出发，沿着图 $ G $ 的边爬行。开始时，它的体力为 $ 1 $。每爬过一条边，它的体力都会下降为原来的 $ \rho $ 倍，其中 $ \rho $ 是一个给定的小于 $1$ 的正常数。而蚂蚁爬到某个顶点时的幸福度，是它当时的体力与该点权值的乘积。

我们把蚂蚁在爬行路径上幸福度的总和记为 $ H $。很显然，对于不同的爬行路径，$H $ 的值也可能不同。小 Z 对 $ H $ 值的最大可能值很感兴趣，你能帮助他计算吗？注意，蚂蚁爬行的路径长度可能是无穷的。

输入格式

每一行中两个数之间用一个空格隔开。

第一行包含两个正整数 $ n , m $，分别表示 $ G $ 中顶点的个数和边的条数；

第二行包含 $ n $ 个非负实数，依次表示 $ n $ 个顶点权值 $ w(1) , w(2) ,\cdots , w(n) $；

第三行包含一个正整数 $ v_0 $，表示给定的起点；

第四行包含一个实数 $ \rho $，表示给定的小于 $1$ 的正常数；

接下来 $m $ 行，每行两个正整数 $ x,y $，表示 $x\to y$ 是 $ G $ 的一条有向边。可能有自环，但不会有重边。

输出格式

仅包含一个实数，即 $ H $ 值的最大可能值，四舍五入到小数点后一位。

样例

input

5 5
10.0 8.0 8.0 8.0 15.0
1
0.5
1 2
2 3
3 4
4 2
4 5

output

18.0

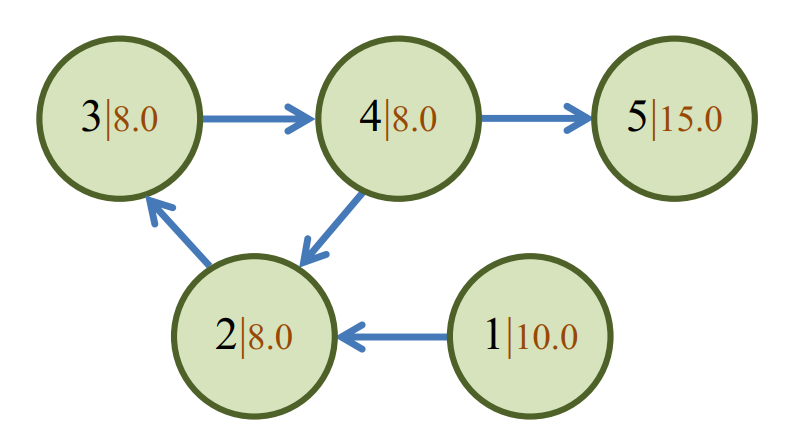
当蚂蚁的爬行路径为 $1\to 2\to 3\to 4\to 2\to 3\to 4\to \cdots \to 2\to 3\to 4\to \cdots$ 时，$H = 10.0+8.0\times 0.5+8.0\times 0.5^2+\cdots $。可以证明， 这个无穷序列的总和为 $18.0$， 且这就是 $H$ 的最大值。

另外，若本样例中 $w(5)$ 改为 $17.0$，其余数据不变，则当路径为 $1\to 2\to 3\to 4\to 5$ 时，$H = 18.0625$。可以证明，这就是此时 $H$ 的最大值。

数据范围与提示

对于 $20\%$ 的数据，$\rho \le 0.5$；
另有 $20\%$ 的数据，保证 $H$ 的最大值在有限路径上取到；
对于 $100\%$ 的数据，$1\le n \le 100, 1\le m \le 1000, 0\lt \rho \le 1 -10 ^{-6},0\le w(i) \le 100$。