题目描述

译自 POI 2007 Stage 1.「Tourist Attractions」

给定 $n$ 个顶点和 $m$ 条边组成的一张图，边有长度，且要求按照一定的顺序停留 $2 \ldots k+1$ 共 $k$ 个点（可以经过这些点但不停留），求最短的符合要求的从 $1$ 出发到 $n$ 的路径。保证存在这样的路径。

输入格式

第一行有三个数 $n$，$m$ 和 $k$，且保证 $k \le n - 2$.

接下来 $m$ 行每行三个整数 $p_i, q_i, l_i (1 \le p_i \lt q_i \le n, 1 \le l_i \le 1\ 000)$，表示一条连接 $p_i$ 和 $q_i$ 的长度为 $l_i$ 的边。

接下来一行一个整数 $g (0 \le g \le \frac{k(k+1)}2)$，表示有 $g$ 条对这 $k$ 个点访问顺序的限制条件。

接下来 $g$ 行每行有两个整数 $r_i$ 和 $s_i$，表示一条要求，先在 $r_i$ 停留，后在 $s_i$ 停留。

输出格式

输出满足要求的路径的最短长度。

样例

input

8 15 4
1 2 3
1 3 4
1 4 4
1 6 2
1 7 3
2 3 6
2 4 2
2 5 2
3 4 3
3 6 3
3 8 6
4 5 2
4 8 6
5 7 4
5 8 6
3
2 3
3 4
3 5

output

19

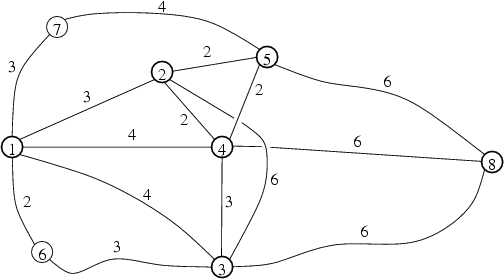
上图为与样例对应的图。要求在 $2,3,4,5$ 四个节点停留，且 $2$ 号点需要在 $3$ 号点之前停留，$4$ 号点和 $5$ 号点需要在 $3$ 号点之后停留。最短的从 $1$ 到 $n$ 的路径为 $1, 2, 4, 3, 4, 5, 8$ 且长度为 $19$。注意可以经过 $2,3,4,5$ 号点而不停留，这样就不会违反限制。

数据范围与提示

$2 \le n \le 20\ 000, 1 \le m \le 200\ 000, 0 \le k \le \min(n-2,20)$